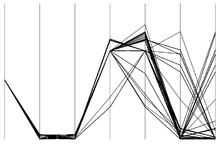
- Coordonnées parallèles
-
Les coordonnées parallèles sont une technique permettant de visualiser un nombre important d'informations de façon non ambiguë.
Exemple de tracé en coordonnées parallèles
Sommaire
Principe
Un espace de dimension n est représenté par n axes parallèles sur un plan, chaque axe représentant une dimension.
Pour représenter un point
de l'espace de dimension n, on place sur les axes parallèles les points Mi d'ordonnée égale à sa coordonnée correspondante xi. Le point M est alors représenté par la ligne brisée reliant les Mi.Ainsi, le point M(18,42,12) de l'espace est représenté par une ligne brisée reliant les points M1(1,18),M2(2,42),M3(3,12).
Histoire
Inventées par Maurice d'Ocagne en 1885[1], elles ont été redécouvertes en 1959 par Alfred Inselberg. Ce système est maintenant utilisé pour la détection de collision d'avions lors du contrôle du trafic aérien, ainsi que pour la recherche d'information lorsque celle-ci est trop volumineuse.
On trouve récemment des applications dans les systèmes de détection d'intrusions.
Nombre de dimensions
Ajouter plus de dimensions dans un graphe de coordonnées parallèles (souvent abrégé en coords-|| ou PC) nécessite simplement de rajouter plus d'axes. L'intérêt des coordonnées parallèles se trouve dans le fait que certaines propriétés géométriques de plusieurs dimensions se transforment facilement en 2D. Par exemple, une série de points sur une ligne dans n-plans se transforme en une série de lignes dans les coordonnées parallèles se faisant intersection à n-1 points. Lorsque n = 2, cela montre une dualité point ↔ ligne éclairant pourquoi les fondations mathématiques des coordonnées parallèles sont développées sur une projection plutôt que dans l'espace Euclidien.
Sont aussi connus les motifs correspondant aux (hyper)surfaces, courbes, plusieurs (hyper)surfaces adoucies, les proximités, les convergences et divergences ainsi que le non-orientabilité[2].
Il devient alors aisé de repérer les corrélations possibles entre les différents évènements (groupes de variables).
Voir aussi
- Les logiciels GGobi (en) et Picviz [3], qui permettent de produire de tels graphiques.
- Une explication interactive[4] des coordonnées Ocagne faite avec CaRMetal
Références
- d'Ocagne, Maurice, Coordonnées Parallèles et Axiales: Méthode de transformation géométrique et procédé nouveau de calcul graphique déduits de la considération des coordonnées parallèles, Paris: Gauthier-Villars, 1885
- (en) A. Inselberg, Parallel Coordinates: VISUALMultidimensional Geometry and its Applications, Springer, 2007
- http://www.wallinfire.net/picviz
- http://db-maths.nuxit.net/CaRMetal/user_galery/diapos/ocagne/
Bibliographie
- Maurice d'Ocagne, Coordonnées parallèles et axiales: Méthode de transformation géométrique et procédé nouveau de calcul graphique déduits de la considération des coordonnées parallèles. Cornell University Library (1885), (ISBN 978-1429700979)
- Sebastien Tricaud, Picviz: Finding a Needle in a Haystack. First Usenix Workshop on the Analysis of System Logs, 2008. PDF paper
Wikimedia Foundation. 2010.
