Constructions Du Milieu D'un Segment
- Constructions Du Milieu D'un Segment
-
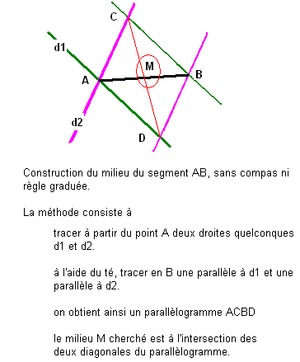
Constructions du milieu d'un segment
à la règle et au té-virtuel, sans compas ni règle graduée
-
- Le té-virtuel est un instrument de dessin qui permet de tracer une parallèle à une droite quelconque passant par un point quelconque.
- Nous n'avons pas besoin de situer la figure dans un plan métrique, il suffit de travailler dans un espace affine. Un tel type de plan ignore les distances, les cercles et les angles droits, il ne connaît que le parallèlisme. Un tel type de plan ignore encore les vecteurs, a fortiori les barycentres et encore plus l'isobarycentre. Il ignore les carrés, les rectangles, les losanges, il ne connaît que les parallèlogrammes. Et dans un parallèlogramme les diagonales se coupent en un point que l'on appelle "milieu", plus exactement "milieu-affine".
à la règle et au compas
La méthode dans ce cas est de construire au compas la médiatrice du segment, le milieu étant l'intersection du segment avec sa médiatrice.
 Portail de la géométrie
Portail de la géométrie
Catégorie : Construction géométrique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Constructions Du Milieu D'un Segment de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Constructions du milieu d'un segment — La construction du milieu d un segment peut s effectuer à l aide d outils très simples . Le milieu I d un segment peut être défini comme le point situé sur le segment [AB] à égale distance de A et de B, ce qui fait du milieu un objet de la… … Wikipédia en Français
Milieu d'un segment — Pour les articles homonymes, voir Milieu. Le milieu d un segment est le point de ce segment situé à égale distance de ses extrémités. Sommaire 1 Symétrie centrale 2 … Wikipédia en Français
Théorème de Mohr-Mascheroni — En géométrie classique plane, le théorème de Mohr Mascheroni, démontré par Georg Mohr en 1672 et par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas… … Wikipédia en Français
Construction D'une Parabole Tangente Par Tangente — Sommaire 1 Exemples 1.1 Explication de cette méthode 1.2 Fonction homographique mise en jeu 1.3 Variante en géométrie projective … Wikipédia en Français
Construction d'une parabole tangente par tangente — Sommaire 1 Exemples 1.1 Explication de cette méthode 1.2 Fonction homographique mise en jeu 1.3 Variante en géométrie projective … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Construction (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot construction peut désigner différentes notions. Sommaire 1 Construction à caractère matériel 2 … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Nombre constructible — Un nombre constructible à la règle et au compas est la mesure d une longueur associée à deux points constructibles à la règle (non graduée) et au compas. Ainsi, est un nombre constructible, mais ni ni π ne le sont. C est du moins ainsi que le… … Wikipédia en Français
Nombre Constructible — Un nombre constructible à la règle et au compas est la mesure d une longueur associée à deux points constructibles à la règle et au compas. Ainsi, est un nombre constructible, mais ni ni π ne le sont. C est du moins ainsi que le définissaient les … Wikipédia en Français