Construction de l'angle moitie
- Construction de l'angle moitie
-
Construction de l'angle moitié
Soit un angle de sommet O dont on souhaite construire l'angle moitié sans utiliser le rapporteur.
- OUTILS AUTORISES: règle, compas.
- (OUTILS INTERDITS: rapporteur, c'est là le défi.)
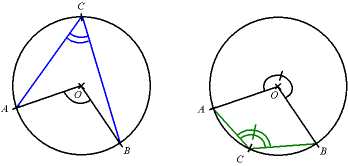
- Il suffit de tracer un cercle de centre O et de rayon quelconque qui coupe les demi-droites de l'angle en A et B, puis de prendre un point C sur le cercle; l'angle moitié sera ACB.
- remarque: il faut prendre le point C sur la bonne partie du cercle, sinon on obtiendrait le supplémentaire de l'angle moitié.
Voir aussi
Pour approfondir
On pourrait souhaiter la généralisation de ce type de constructions, diviser un angle en 3, 5 , 7 etc, mais il a été démontré que la trisection de l'angle fait partie des problèmes impossibles à résoudre à la règle et au compas.
 Portail de la géométrie
Portail de la géométrie
Catégories : Construction géométrique | Angle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Construction de l'angle moitie de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Construction De L'angle Moitié — Soit un angle de sommet O dont on souhaite construire l angle moitié sans utiliser le rapporteur. OUTILS AUTORISES: règle, compas. (OUTILS INTERDITS: rapporteur, c est là le défi.) Il suffit de tracer un cercle de centre O et de rayon quelconque… … Wikipédia en Français
Construction de l'angle moitié — Soit un angle de sommet O dont on souhaite construire l angle moitié sans utiliser le rapporteur. OUTILS AUTORISES: règle, compas. (OUTILS INTERDITS: rapporteur, c est là le défi.) Il suffit de tracer un cercle de centre O et de rayon quelconque… … Wikipédia en Français
Construction (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot construction peut désigner différentes notions. Sommaire 1 Construction à caractère matériel 2 … Wikipédia en Français
Construction a la regle et au compas — Construction à la règle et au compas Euclide a fondé sa géométrie sur un système d axiomes qui assure en particulier qu il est toujours possible de tracer une droite passant par deux points donnés et qu il est toujours possible de tracer un… … Wikipédia en Français
Construction À La Règle Et Au Compas — Euclide a fondé sa géométrie sur un système d axiomes qui assure en particulier qu il est toujours possible de tracer une droite passant par deux points donnés et qu il est toujours possible de tracer un cercle de centre donné et passant par un… … Wikipédia en Français
Angle aigu — Angle Pour les articles homonymes, voir Angles. En géométrie, la notion générale d angle se décline en plusieurs concepts apparentés. Dans son sens ancien, l angle est une figure plane, portion de plan délimitée par deux droites sécantes. C est… … Wikipédia en Français
Angle entre deux droites — Angle Pour les articles homonymes, voir Angles. En géométrie, la notion générale d angle se décline en plusieurs concepts apparentés. Dans son sens ancien, l angle est une figure plane, portion de plan délimitée par deux droites sécantes. C est… … Wikipédia en Français
Angle nul — Angle Pour les articles homonymes, voir Angles. En géométrie, la notion générale d angle se décline en plusieurs concepts apparentés. Dans son sens ancien, l angle est une figure plane, portion de plan délimitée par deux droites sécantes. C est… … Wikipédia en Français
Angle obtus — Angle Pour les articles homonymes, voir Angles. En géométrie, la notion générale d angle se décline en plusieurs concepts apparentés. Dans son sens ancien, l angle est une figure plane, portion de plan délimitée par deux droites sécantes. C est… … Wikipédia en Français
Angle plat — Angle Pour les articles homonymes, voir Angles. En géométrie, la notion générale d angle se décline en plusieurs concepts apparentés. Dans son sens ancien, l angle est une figure plane, portion de plan délimitée par deux droites sécantes. C est… … Wikipédia en Français

