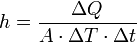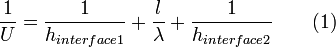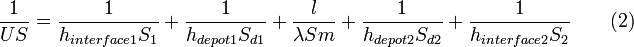Coefficient de transmission thermique U

Coefficient de transmission thermique U

Coefficient de transfert thermique

Le coefficient de transfert thermique est un flux thermique au travers d'une surface d'échange. Il permet de calculer l'intensité de l'énergie échangée par unité de surface et unité de temps en fonction de la différence de température de part et d'autre de la surface d'échange. C'est un terme important dans l'équation d'un transfert thermique et permet d'indiquer la facilité avec laquelle l'énergie thermique passe au travers de la surface d'échange.

Sommaire

Définition

Mathématiquement on le définit de la manière suivante :

h = \frac{\Delta Q}{A \cdot \Delta T \cdot \Delta t}

avec

  • ΔQ - énergie transférée
  • h - coefficient de transfert thermique
  • A - surface d'échange
  • ΔT - différence de température de part et d'autre de la surface d'échange
  • Δt - intervalle de temps

Dans le système SI, les unités de ce coefficient sont W/m2K. L'inverse du coefficient de transfert thermique correspond à la résistance thermique.

Coefficient de transfert thermique global

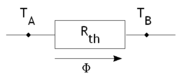
Dans le cas d'une interface complexe composée de plusieurs surfaces d'échange placées en parallèle, il est possible d'additionner les coefficients pour obtenir le coefficient de transfert global de part et d'autre de l'interface. Ceci est particulièrement utilisé dans les échangeurs de chaleur où l'on trouve 2 interfaces et une résistance due à la paroi qui sépare les 2 fluides. L'addition se calcule en prenant la somme des inverses des différents coefficients avec les différentes résistances à la manière de l'addition des résistances électriques (en supposant que le flux est unidirectionnel).

Analogie du transfert thermique avec le courant électrique

Le coefficient de transfert global est en général noté U (Uw pour les vitrages), et pour les coefficients de transfert locaux ou de film, le symbole h est utilisé[1].

\frac{1}{U} = \frac{1}{h_{interface1}} + \frac{l}{\lambda}+ \frac{1}{h_{interface2}} \qquad (1)

avec :

  • U - coefficient de transfert thermique global
  • hinterface1 - coefficient de transfert thermique de film interne
  • hinterface2 - coefficient de transfert thermique de film externe
  • l - épaisseur du matériau séparant les 2 phases
  • λ - conductivité thermique du matériau

Toutefois ceci n'est valable que pour un cas idéal sans dépôt sur la surface d'échange qui augmente la résistance au transfert et pour une surface plane. Le cas plus général est donné par l'équation (2)[2]

\frac{1}{US} = \frac{1}{h_{interface1} S_1} + \frac{1}{h_{depot1} S_{d1}} + \frac{l}{\lambda Sm} + \frac{1}{h_{depot2}S_{d2}} + \frac{1}{h_{interface2}S_2} \qquad (2)

Notes et références

  1. ↑ Perry, R.H., Green, D.W., Perry's Chemical Engineers' Handbook, McGraw-Hill, 1997, 2581 p. (ISBN 9780070498419), « 11 », p. 11-24 
  2. ↑ A. Bejan, A.D.Kraus, Heat Transfer Handbook, John Wiley & Sons, 2003, 1480 p. (ISBN 9780471390152), « 11 », p. 799-804 

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Coefficient de transfert thermique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coefficient de transmission thermique U de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • coefficient de transmission thermique — šilumos perdavimo koeficientas statusas T sritis fizika atitikmenys: angl. coefficient of heat transmission; heat transmission coefficient vok. Wärmedurchgangskoeffizient, m rus. коэффициент теплопередачи, m pranc. coefficient de transmission de… …   Fizikos terminų žodynas

  • coefficient de transmission thermique de surface — paviršiaus šilumos perdavos koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. surface coefficient of heat transfer rus. коэффициент поверхностной… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • coefficient de transmission thermique de surface — paviršiaus šilumos perdavos koeficientas statusas T sritis fizika atitikmenys: angl. surface coefficient of heat transfer vok. Wärmeübergangskoeffizient der Oberfläche, m rus. коэффициент поверхностной теплопередачи, m pranc. coefficient de… …   Fizikos terminų žodynas

  • coefficient de transmission de la chaleur — šilumos perdavimo koeficientas statusas T sritis fizika atitikmenys: angl. coefficient of heat transmission; heat transmission coefficient vok. Wärmedurchgangskoeffizient, m rus. коэффициент теплопередачи, m pranc. coefficient de transmission de… …   Fizikos terminų žodynas

  • coefficient of heat transmission — šilumos perdavimo koeficientas statusas T sritis fizika atitikmenys: angl. coefficient of heat transmission; heat transmission coefficient vok. Wärmedurchgangskoeffizient, m rus. коэффициент теплопередачи, m pranc. coefficient de transmission de… …   Fizikos terminų žodynas

  • THERMIQUE — La thermique est la branche de la physique qui traite des échanges de chaleur accompagnés ou non d’échange de masse et de changement de phases. Elle peut donc être considérée comme partie intégrante de la thermodynamique des phénomènes… …   Encyclopédie Universelle

  • heat transmission coefficient — šilumos perdavimo koeficientas statusas T sritis fizika atitikmenys: angl. coefficient of heat transmission; heat transmission coefficient vok. Wärmedurchgangskoeffizient, m rus. коэффициент теплопередачи, m pranc. coefficient de transmission de… …   Fizikos terminų žodynas

  • surface coefficient of heat transfer — paviršiaus šilumos perdavos koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. surface coefficient of heat transfer rus. коэффициент поверхностной… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • surface coefficient of heat transfer — paviršiaus šilumos perdavos koeficientas statusas T sritis fizika atitikmenys: angl. surface coefficient of heat transfer vok. Wärmeübergangskoeffizient der Oberfläche, m rus. коэффициент поверхностной теплопередачи, m pranc. coefficient de… …   Fizikos terminų žodynas

  • Isolation thermique — Pour les articles homonymes, voir isolation. L isolation thermique désigne l ensemble des techniques mises en œuvre pour limiter les transferts de chaleur entre un milieu chaud et un milieu froid. On retrouve de l isolation thermique dans :… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”