Choc mecanique

Un choc mécanique intervient lorsque dans un système mécanique une force, une position, une vitesse ou une accélération est brusquement modifiée.

Quand il s'agit de deux objets solides, on préfère parler de percussion mécanique.

Ici, il sera traité de choc entre particules classiques. Sinon voir choc relativiste: la réaction d'instabilité du neutron { n → p ⁺ + e ⁻ + ν }(Fermi, 1930) est incompréhensible en mécanique classique.

Le niveau initial sera élémentaire (correspondant à 15-16 ans)

Pour un niveau supérieur, une étude complète et moderne du choc général entre deux corps (de masses inégales, d'élasticité imparfaite et avec frottement) est disponible en http://www.regispetit.com/bil_pra.htm (article Pour la Science).

Sommaire 1 choc élastique sur une droite 1.1 Expérience princeps (dite symétrique) 1.2 le Principe de Relativité 1.3 Déduction 2 le cas des masses inégales 2.1 le cas m1=3m ;m2=m 2.2 le cas général 3 Histoire des sciences 4 Explosion d'un obus en 2 masses m1 et m2 5 Choc élastique de 2 particules 6 Section efficace 7 Voir aussi

choc élastique sur une droite

Soient deux points matériels M1 et M2, de masse m1 et m2 (on pose M := m1+m2), de vitesse V1 et V2 avant le choc.

Problème : déterminer leur vitesse, W1 et W2 après le choc.

Ainsi se posait le problème, au tout début de la mécanique. Descartes avait proposé (1644) une solution fausse, que Huygens corrigea (vers 1652); mais sera donnée ici sa version de 1669.

Comme Descartes le suggère en toutes choses, il faut commencer par le SIMPLE : ici m1 = m2 = m . Par simple raison d'homogénéité, la masse s'efface et laisse à résoudre un simple problème de cinématique.

Expérience princeps (dite symétrique)

Soit l'expérience dite (S) pour Symétrique :

État Initial { v1 = u et v2 = - u}.

Le point milieu O reste immobile et l'évidence indique par raison de symétrie qu'il le restera. D'où:

État Final {w1= -x et w2 = x}.

La symétrie temporelle t/-t implique alors x = u, sinon on pourrait indéfiniment augmenter l'énergie des 2 particules par itération.

donc (S): E.I.{u;-u} ⇒ E.F.{-u;u}

Malgré la part d'arbitraire dans ces affirmations, tout le monde agrée, vu que l'expérience confirme. Cette analyse sera basique. Huygens part de là en 1652 ( il a 23ans et déjà une grande notoriété en mathématique et logique.

le Principe de Relativité

Entre en jeu la révolution conceptuelle de Galilée (2^e et 6^e journée du Dialogo) : le mouvement uniforme de vitesse V est "comme rien": c’est-à-dire que si on refait l'expérience dans un bateau (le bateau de Huygens diront plus tard les Anglais MacLaurin et Taylor), on doit obtenir les mêmes résultats. Traduisons cela en formules :

Si on connaît UNE expérience de choc, disons (E) :{v1;v2}⇒ {w1= f(v1,v2); w2 = g(v1,v2)}, alors :

pour tout V ,

{v1+V ; v2+V} ⇒ { w1+V = f( v1+V, v2+V); w2+V = g( v1+V, v2+V) }

Ainsi, dit Huygens, on obtient la réponse pour toute la classe des expériences déduites de (E), soit C[(E)] cette classe.

Déduction

Or, on connaît (S) ; donc on connaît C[(S)]. Mais on peut exprimer aisément v1 et v2 à l'aide de u et V ; et donc tous les cas seront résolus ; sitôt dit, sitôt fait :

{u+V ; -u+V} ⇒ {-u+V ; u+V}  soit {w1 = v2 et w2 = v1}

C'est la fameuse loi d'échange des vitesses. En particulier, dit Huygens triomphal: cela explique le cas de la pétanque, le "carreau" : {u;0} ⇒ {0;u}

le cas des masses inégales

le cas m1=3m ;m2=m

Un cas très joli à voir est la solution particulière (E1) : {u;-u} ⇒ {0;2u}

C'est spectaculaire sur des bancs à coussins d'air légèrement inclinés et raboutés : la masse M1 s'arrête et la masse M2 s'en retourne 4 fois plus loin !!

Mais de ce fait, on connaît la classe C[(E1)].Choisissons une autre unité, juste par commodité des calculs ultérieurs : {2u;-2u} ⇒ {0;4u} et DONC {2u+V;-2u+V} ⇒ {V;4u+V}.

Choisissons V = -u, et il vient cette expérience appelée (R): {u;-3u}⇒ {-u;3u}

On reconnaît dans (R) le renversement des vitesses.

Et là, l'intuition géniale parle : est-ce toujours ainsi ?

le cas général

Oui; parce que Descartes l'a dit, un peu ingénument : la quantité de mouvement totale se conserve.

Le cas précédent était 3 m de vitesse u et m de vitesse -3u, c’est-à-dire P = 0.

Bien sûr, Huygens va le voir et le généraliser :

le cas (R) est celui où P =0 :

{m2/M .u ; -m1/M .u} ⇒ renversement des vitesses.

On en déduit la classe C[(R)]:

{m2/M .u + V ; m1/M .u + V} ⇒ {-m2/M .u + V ; -m1/M .u + V }

ce qui permet donc d'avoir la solution générale:

{v1;v2} ⇒ {w1;w2} avec w1 = A.v1 + B.v2 et w2 = C.v1 + B.v2 ,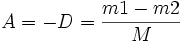

 ;  ,

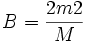on laisse au lecteur le soin de deviner C.

Pour des lecteurs avertis, tous ces raisonnements sont valables en relativité restreinte, puisque la logique y est parfaite, mais c'est l'addition des vitesses qu'Einstein modifiera.

Histoire des sciences

En 1654, Huygens a vraisemblablement terminé ce travail (allégé ici par les notations algébriques qui n'existent pas à l'époque). Il dit qu'il a trouvé en 1656. Mais il ne publie pas : c'est la règle à l'époque ; publier c'est périr, car immanquablement l'autre vous rattrape et vous double.

Après consécration pour d'autres travaux mathématiques, il est la Vedette des salons en décembre 1660 à Paris, en janvier à Londres; car il est capable de répondre à n'importe quel choc frontal de boules ( on opérait alors avec des boules à suspension bifilaire, comme on en voit dans certains magasins de gadgets).

Mais il sait qu'il n'a pas fini :

• il va découvrir comme une loi "admirable" que lors du choc, RIEN NE SE PASSE pour un certain Point G, dit centre de masse : il reste imperturbablement à vitesse constante : preuve qu'il n'a pas compris que P = M V_G.
• il ne sait toujours rien de la force-percussion. Il sait seulement que ΔP₁ = − ΔP₂ : il faudra attendre Newton pour aller plus loin.
• Il retrouve avec satisfaction que l'énergie cinétique ( de Torricelli) se conserve. Mais il est perdu quand les chocs sont inélastiques: doit-on conserver P ou l'énergie ?

Évidemment, les chocs non frontaux sont hors de portée, les vecteurs ne sont pas vraiment créés.

Explosion d'un obus en 2 masses m1 et m2

C'est le cas le plus simple : tout reste dans un plan. On néglige pour l'instant la gravité: tout a lieu dans un temps infiniment court.

L'obus ayant une vitesse V on se place dans le référentiel galiléen R* où V = 0 : donc P* = 0

Donc les deux quantités de mouvements sont p. 1* = -(p. 2*)/2.5 = p* et l'énergie cinétique p*²/2(1/m1+1/m2) = Q =énergie de l'explosion (forcément positive). On en déduit v1* et v2* d'où v1= v1* + V

La direction de v1 n'est donc pas v1* : c'est le phénomène d'aberration usuelle (penser à la pluie).

Si l'on fait intervenir la gravité uniforme, on trouve que le centre de masse des fragments suit la trajectoire qu'aurait eu G si l'obus n'avait pas explosé : ceci n'est pas vrai pour un satellite! (erreur commune).

Choc élastique de 2 particules

Dans R*, l'énergie p*²/2m ( avec 1/m = 1/m1 +1/m2) se conserve donc le module de p* aussi, donc

p. 1 = p'* + P. m1/M et p. 2 = -p'* + P. m2/M, l'orientation de p'* restant indéterminée sans autre précision.

Si les masses sont égales et M2 au repos, M1 et M2 repartent à angle droit ( c'est la règle dite du billard sans effet, cf billard). Par contre si m1>m2, M1 ne peut reculer et sinθ_1max = m₂ / m₁. Enfin si m1<m2, M1 peut reculer, mais évidemment pas de manière isotrope.

Section efficace

ébauche à finir

ce paragraphe est d'un niveau beaucoup plus élevé.

Il consiste à déterminer pour un point d'impact B dan le plan de section droite de la cible M2, de trouver la trajectoire asymptotique de M1 : on appelle souvent θ cet angle fonction de M2B = b et de la loi d'interaction de potentiel U(r) entre les particules ( loi dite de diffusion (scattering in english).

Mieux encore, à partir des relevés expérimentaux, peut-on inversement déterminer U(r) : problème dit de scattering inverse ( Firsov 1953; puis Lax…): comme dans le cas des puits de potentiel, on sait le faire, via une transformation d'Abel modifiée. référence Landau p. 75).

Mais il faut bien dire que la réalité nucléaire est plus complexe : les vitesses sont relativistes; la mécanique doit de plus être quantique et met parfois en jeu l'indiscernabilité ( cf Feynman à un niveau Licence).

Dans le cas des liquides, où les forces d'attraction de Van der Waals sont en jeu, on comprend bien qu'à faible vitesse, le diamètre apparent des disques d'impact, (4.r), va augmenter : cela explique des variations dues à la température T du libre parcours moyen .

Voir aussi

• Choc élastique
• Choc relativiste
• Collision inélastique
• expérience de Compton
• diffusion de Rutherford
• diffusion quantique de Rutherford
• référence :

C.Villain : Huygens et la Relativité(1988) Huygens : de Motu corporum ex percussione, in œuvres complètes : l'essai de Relativité Totale y est impressionnant; Lorentz a absolument tenu à ce qu'il soit publié.

• Portail de la physique