- Zéros complexes d'équations réelles
-
Rappel principal (cf. théorème de d'Alembert-Gauss) : le degré d'un polynôme P(X) réel est égal au nombre de ses racines (éventuellement) complexes, comptées avec leur multiplicité.
Rappel secondaire ([réf. souhaitée]) : Les racines complexes d'un polynôme réel vont par deux, conjuguées l'une de l'autre.
Autant l'intuition des racines réelles de P(X) est immédiate (ce sont les points de la courbe Y = P(X) qui rencontrent l'axe (ox)), autant l'existence de ces racines complexes peut paraître difficile à acquérir et leur localisation indéterminable intuitivement.
Les complexes, plus généralement, sont des objets mathématiques difficiles à concevoir. Ce fut l'occasion d'une longue lutte entre tenants du réalisme géométrique et formalistes de l'algèbre symbolique[1] (cet article se place du côté du réalisme géométriques).
Une notion proche qui peut être étudiée : les branches réelles de la forme complexe P(Z) (si elles existent), c'est-à-dire, les valeurs complexes, Zi, telles que P(Zi) est réel. Parmi ces valeurs, on retrouvera les zéros de P.
Sommaire
Degré 0, 1
Les cas des polynômes de degré 0 ou 1 sont sans intérêt : un polynôme constant admet aucune ou une infinité de zéros, un polynôme de degré 1 admet une unique racine réelle.
Degré 2
Article détaillé : Équation du second degré.La courbe réelle Y = P2(X) est une parabole, avec 0 ou 2 zéros réels. Le cas où il n'y a qu'un zéro réel correspond à un zéro réel double.
Lorsqu'il y a 0 zéro réel, les deux zéros sont complexes. Si la parabole n'est pas loin de l'axe, on peut avancer, par un argument de continuité, que les zéros complexes ne sont pas loin de l'optimum, mais au fur et à mesure que la parabole s'éloigne de l'axe, quel est le chemin pris par les zéros complexes ?
Notons P2(Z) = pZ2 + qZ + r pour faire quelques calculs.
P2(X + iY) = (r + qX + pX2 − qY2) + i(qY + 2pXY)
Si l'on cherche les points réels, il faut annuler le coefficient imaginaire. On trouve Y = 0, ou X = − q / 2p. C'est-à-dire la courbe réelle et une courbe dans un plan complexe perpendiculaire à l'axe (ox) au point − q / 2p :
P2( − q / (2p) + iY) = − q2 / 4p + r − pY2
Cette courbe est une parabole de direction opposée (-p) à la parabole réelle, qui partage le sommet de cette courbe réelle.
En comptant les zéros de cette courbe et les zéros de la courbe réelle, on trouvera bien 2 zéros, dans tous les cas.
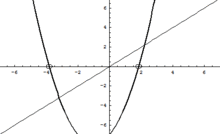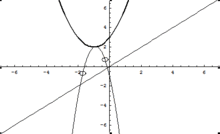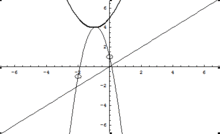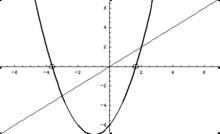
Dans (0x(iy)z), on peut dessiner ces deux courbes pour quelques valeurs de p, q et r par exemple 1, 2 et 3 (en gras la courbe réelle, et il faut imaginer les deux courbes perpendiculaires l'une à l'autre, l'une dans le plan (Oxz), l'autre dans le plan (Oyz)).

et si on anime un peu :

Cette animation illustre également la continuité qu'il existe entre les valeurs des racines et les coefficients de la parabole, que ces racines soient réelles ou complexes et même lorsque l'on se place à l'endroit du passage entre réel et complexe.Enfin, de ce qui précède, on peut comprendre que le milieu entre les deux racines du polynôme est toujours réel, et se situe au niveau de l'extremum de la parabole. C'est ce type de résultat que l'intuition recherchée ici peut apporter.
Ce résultat s'apparente aux résultats obtenus en géométrie avec l'introduction des complexes, comme par exemple l'existence de l'axe radical entre deux cercles quelle que soit la position relative des deux cercles (cf. Warusfel[2], qui argumente ainsi "on est conduit ainsi à une géométrie complexifiée où tout est plus simple"). Des résultats qui, s'ils ne sont pas forcément plus simples à saisir, comportent moins de cas particuliers.Degré 3
La courbe réelle Y = P3(X) a au moins un zéro réel (éventuellement triple), elle peut en avoir 3, ou 2 (avec 1 double). Si elle n'a qu'un seul zéro réel (simple), alors les deux zéros manquants sont complexes (conjugués l'un de l'autre). Lorsque la courbe réelle de Y = P3(X) possède un coude et que ce coude est proche de l'axe (Ox), alors par un argument de continuité, on peut avancer que les zéros complexes sont proches de cet optimal local, mais quand la courbe ne possède pas de coude, ou que le coude est loin de l'axe (ox), où vont les zéros complexes ?
Notons P3(Z) = pZ3 + qZ2 + rZ + s pour faire quelques calculs :
P3(X + iY) = (s + rX + qX2 − qY2 + pX3 − 3pXY2) + i(rY + 2qXY + 3pX2Y − pY3)
Si l'on cherche les points réels, il faut annuler le coefficient imaginaire. On trouve Y = 0, ou Y2 = (r + 2qX + 3pX2) / p. C'est-à-dire la courbe réelle et une courbe complexe symétrique (ce qui assure l'existence de zéros conjugués, si des zéros existent) quand (r + 2qX + 3pX2) / p est positif :
P3(X + iY / / Y2 = (r + 2qX + 3pX2) / p) = − qr / p + s − 2q2X / p − 2rX − 8qX2 − 8pX3
On retrouve deux courbes de degré 3, orientées dans le sens inverse de la courbe réelle (-8p).
Sur un exemple, avec p, q, r ,s égal à 2, 3, 4, 5 (en gras la courbe réelle) :

remarque : ces branches réelles peuvent être discontinues (si (r + 2qX + 3pX2) / p n'est pas positif), il suffit de prendre r et p de signe opposé dans la forme de degré 3 pour que la branche réelle disparaisse autour de X=0 ; et les zéros peuvent 'tomber' dans ces discontinuités. C'est normal, si ces branches existaient toujours, et n'étaient pas discontinues, alors pour P3 avec 3 zéros réelles, il faudrait ajouter 2 zéros complexes sur ces branches réelles, ce qui ferait 5 zéros.
Autre voie de recherche : par le passage au quotient
Quand la courbe réelle n'a qu'un zéro réel (strictement), si l'on trace une droite qui passe par ce zéro avec une pente quelconque (par ex. 1), en prenant le quotient de la courbe réelle par cette droite, on obtient une parabole, c'est confirmé par la théorie et la pratique.
D'après ce qui précède, cette parabole a 2 zéros (réels ou complexes), qui sont des zéros réels de la courbe de degré 3. Cela donne les zéros réels, mais pas les éventuelles branches réelles de la courbe complexe. (la branche réelle de la parabole complexe, qui donne les zéros complexes, n'est pas la branche réelle de la forme de degré 3, car il faut (re)multiplier cette courbe par la droite quotient pour revenir à la courbe de degré 3, et on sort alors des réels).
Degré 4
Contrairement au degré 3, il n'y a pas forcément une racine réelle. Toutes les racines peuvent être complexes.
Les résultats pour le degré 4 ressemble à ceux pour le degré 3 : existence de branches réelles sous forme de courbes complexes solution d'équation en Y2. Ces courbes sont donc symétriques, et elles peuvent avoir des discontinuités. Les branches sont orientées dans le sens inverse de la courbe réelle.
Contrairement au degré 3, il n'y a pas forcément une racine réelle, il n'y a donc pas de méthode alternative par passage au quotient.
Conclusion
La visualisation des branches réelles pour le degré 2 est intéressante et apporte l'information recherchée : où sont les racines complexes.
La visualisation des branches réelles pour le degré 3, 4 et + -quand elle est possible- n'apporte pas beaucoup, même si elle peut indiquer -quand elle est possible- où sont les racines complexes. La visualisation par la méthode du quotient donne quelques résultats, mais elle n'est pas complètement intuitive (la courbe dérivée est plus intuitive) et ne se généralisera pas aux degrés pairs sans racine réelle.
Les branches réelles ne sont pas toujours définies (il suffit de prendre r et p de signe opposé dans la forme de degré 3 pour que la branche réelle disparaisse autour de X=0).
Notes et Références
- Dahan-Dalmedico, A. et Peiffer, J., Une histoire des mathématiques, Points Sciences, Seuil Ed.
- Warusfel, A., Les nombres et leurs mystères, Points Sciences, Seuil Ed.
Articles connexes
Wikimedia Foundation. 2010.