Transducteur à états finis

Transducteur à états finis

En informatique théorique, en linguistique, et en particulier en théorie des automates, un transducteur fini (appelé aussi transducteur à états finis par une traduction maladroite de l'anglais finite state transducer) est un automate fini avec sorties. C'est une extension des automates finis. Ils opèrent en effet sur les mots sur un alphabet d'entrée et, au lieu de simplement accepter ou refuser le mot, ils le transforment, de manière parfois non déterministe, en un ou plusieurs mots sur un alphabet de sortie. Ceci permet des transformations de langages, et aussi des utilisations variées telles que notamment l'analyse syntaxique.

Une des propriétés remarquables des transducteurs finis est qu'ils transforment les langages rationnels en langages rationnels, et les langages algébriques en langages algébriques.

Sommaire

Définitions formelles

Transducteur fini

Un transducteur fini est défini par un 6-uplet T = (Σ1 , Σ2 , Q , I , F , δ), où :

  • Σ1 l' alphabet d'entrée
  • Σ2 l' alphabet de sortie
  • Q l'ensemble fini des états du transducteur
  • I l'ensemble des états initiaux \subseteq Q
  • F l'ensemble des états finals \subseteq Q
  • δ la table de transition : c'est un sous-ensemble de Q \times (\Sigma_{1}\cup\{\varepsilon\}) \times (\Sigma_{2}\cup\{\varepsilon\}) \times Q où ε est le mot vide.

La propriété (q,a,b,r) \in \delta signifie qu'il existe une transition de l'état q vers l'état r par laquelle on lit le symbole a \in \Sigma_{1}\cup\{\varepsilon\} et on écrit le symbole b \in \Sigma_{2}\cup\{\varepsilon\}. Ceci est fréquemment représenté par l'écriture

q\xrightarrow{a|b}r

Le symbole a est l' étiquette d'entrée, le symbole b est l' étiquette de sortie de la transition. On note comme d'usage

  • \Sigma^{*}_{1} le monoïde libre des mots sur l'alphabet d'entrée
  • \Sigma^{*}_{2} le monoïde libre des mots sur l'alphabet de sortie


Clôture transitive

La clôture transitive δ * de δ est la plus petite relation vérifiant :

  • \delta^{*} \subseteq Q \times \Sigma^{*}_{1} \times \Sigma^{*}_{2} \times Q
  • \delta \subseteq \delta^{*}
  • \forall q \in Q, (q,\varepsilon,\varepsilon,q) \in \delta^{*} (réfléxivité)
  • Si (q,x,y,r) \in \delta^{*} et (r,a,b,s) \in \delta, alors (q,xa,yb,s) \in \delta^{*} (transitivité)

En d'autres termes, (q,x,y,r) \in \delta^{*} signifie qu'il existe un chemin de l'état q vers l'état r dont l'étiquette d'entrée est le mot x \in \Sigma^{*}_{1} et l'étiquette de sortie est le mot y \in \Sigma^{*}_{2}. Un chemin est réussi si q\in I et r\in F.

Relation rationnelle

Par analogie avec les automates à états finis qui reconnaissent un langage, un transducteur fini T reconnaît une relation, notée [T] du produit cartésien des deux monoïdes libres. On a (x,y)\in [T] ou x[T]y si et seulement s'il existe p \in I et r \in F tel que (p,x,y,r) \in \delta^{*}. En d'autres termes, x est en relation avec y si et seulement s'il existe un chemin réussi qui lit x et écrit y.

Variante de définition

Au lieu de demander que les étiquettes des transition sont des lettres ou le mot vide, on autorise comme étiquettes des mots sur l'alphabet d'entrée resp. l'alphabet de sortie.

Les différentes façons de considérer un transducteur fini

Un transducteur fini peut être vu de plusieurs façons, ce qui permet des utilisations tout à fait différentes.

Transducteur vu comme un automate

Dans le cas où il aucune des étiquettes du transducteur n'est le mot vide, on peut voir un transducteur comme un cas particulier des automates finis. Il vérifie alors les propriétés classiques des automates.

Il suffit en effet de considérer un automate dont l'alphabet est le produit cartésien des deux alphabets : \Sigma = \Sigma_{1} \times \Sigma_{2}.

Transducteur vu comme une relation rationnelle

Le fait de considérer un transducteur comme une relation rationnelle permet d'établir une propriété primordiale dans l'étude et l'utilisation de ceux-ci : la clôture par composition.

Opérations sur les transducteurs

Opérations héritées des automates

  • Union : soient A et B deux transducteurs finis. La relation [A \cup B]=[A] \cup [B]

définit un transducteur fini, noté A \cup B.

  • Produit de concaténation : soient A et B deux transducteurs, alors il existe un transducteur noté A \cdot B tel que xx'[A \cdot B]yy' si et seulement si x[A]y et x'[B]y'. En d'autres termes, [A \cdot B]=\{(xx',yy')\mid (x,y)\in [A], (x',y')\in[B]\}.


  • Intersection : l'intersection de deux relations R et R' est la relation R'' définie par

R''=R\cap R'. Même si R'' et R'' sont des relations rationnelles, leur intersection n'est pas nécessairement une relation rationnelle.

Composition

Considérons deux transducteurs finis T1 et T2 tels que l'alphabet de sortie de T1 coïncide avec l'alphabet d'entrée de T2.

Le composé T_{3} = T_{2} \circ T_{1} est défini par la relation [T3] :

x[T_{3}]y \Leftrightarrow \exists z tel que x[T1]z et z[T2]y.

Il est important de noter que la composition de deux transducteurs finis est encore un transducteur fini. Ainsi la composition permet d'élaborer facilement des transducteurs ayant une fonction complexe à partir de transducteurs simples.

Projections

  • Projection gauche : la projection gauche d'une relation R est l'ensemble K=\{x\mid \exists y: (x,y)\in R\}. Soit T un transducteur fini. La projection gauche de la relation [T] est un langage rationnel: il existe automate fini qui la reconnaît; il suffit en effet d’« oublier » les étiquettes de sortie sur les transitions de T.
  • Projection droite : de même, la projection droite d'une relation rationnelle est un langage rationnel.

Application à l'analyse grammaticale

L'opération de composition permet de créer très facilement un transducteur qui, à partir d'une séquence de lettres (une phrase) reconnaît la fonction grammaticale de chaque mot.

Pour cela on définit deux transducteurs :

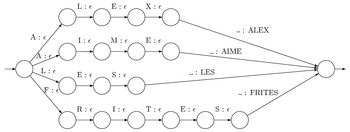
  • Un transducteur L (Lexique) qui transforme une séquence de lettres suivies d'un espace en un mot.
Un exemple de Lexique.
Un exemple de Lexique.
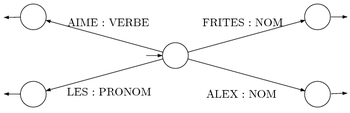
  • Un transducteur D (Dictionnaire) qui transforme un mot en sa fonction grammaticale (ou éventuellement plusieurs si le mot est ambigüe).
Un exemple de Dictionnaire
Un exemple de Dictionnaire

Il suffit ensuite de considérer le transducteur composé T = D^{*} \circ L^{*} Comme la composition préserve la fonction des transducteurs, ce nouveau transducteur prendra en entrée une séquence de lettres, et écrira en sortie une séquence de fonctions grammaticales correspondants aux mots de la phrase.

Extension du modèle : transducteur fini pondéré

De même que pour les automates finis, les transducteurs finis peuvent être améliorés en les pondérant. La méthode est d'ailleurs identique à celle utilisée pour les automates fini pondérés.

Une telle optimisation peut se voir utilisée par exemple dans des correcteurs d'orthographe. Pour cela, il suffit de définir une distance entre les mots comme par exemple d(u,v) = nombre de modifications nécessaires pour transformer u en v. Il suffit alors de définir un transducteur qui réalise des transformations élémentaires (changement de lettre, ajout d'une lettre, suppression d'une lettre) en pondérant correctement ces transformations.

Ainsi, à chaque fois qu'un mot n'existe pas dans le dictionnaire, une comparaison de ce mot aux autres par l'intermédiaire du transducteur pondéré déterminera quel mot correct est le plus proche.

Articles connexes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transducteur à états finis de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Automate fini — Pour les articles homonymes, voir Automate. Fig. 1 : Automate fini reconnaissant les écritures binaires des multiples de 3. Un automate fini (on dit parfois, par une traduction littér …   Wikipédia en Français

  • Compilateur — Pour les articles homonymes, voir Compilation. Un compilateur est un programme informatique qui traduit un langage (appelé le langage source) en un autre (le langage cible), généralement dans le but de créer un exécutable. Un compilateur sert le… …   Wikipédia en Français

  • Automate sur les mots infinis — En informatique théorique, et spécialement en théorie des automates un automate sur les mots infinis ou ω automate est un automate fini, déterministe ou non, qui accepte des mots infins. Comme un tel automate ne s arrête pas, les conditions d… …   Wikipédia en Français

  • Automate cellulaire — À gauche, une règle locale simple : une cellule passe d un état (i) au suivant (i+1) dans le cycle d états dès que i+1 est présent dans au moins 3 cellules voisines. À droite, le résultat (complexe) de l application répétée de cette règle… …   Wikipédia en Français

  • Théorème de Kleene —  Ne doit pas être confondu avec Théorème de récursion de Kleene ni Théorème du point fixe de Kleene. En informatique théorique, et plus précisément en théorie des automates, le théorème de Kleene affirme qu un langage peut être décrit par… …   Wikipédia en Français

  • Effet piézo-électrique — Piézoélectricité Illustration du comportement d’une pastille piézoélectrique : la contrainte appliquée crée un signal électrique. La piézoélectricité (du grec piézein presser, appuyer) est la propriété que possèdent certains corps de se… …   Wikipédia en Français

  • Piezoelectricite — Piézoélectricité Illustration du comportement d’une pastille piézoélectrique : la contrainte appliquée crée un signal électrique. La piézoélectricité (du grec piézein presser, appuyer) est la propriété que possèdent certains corps de se… …   Wikipédia en Français

  • Piezoélectricité — Piézoélectricité Illustration du comportement d’une pastille piézoélectrique : la contrainte appliquée crée un signal électrique. La piézoélectricité (du grec piézein presser, appuyer) est la propriété que possèdent certains corps de se… …   Wikipédia en Français

  • Piezzo-électrique — Piézoélectricité Illustration du comportement d’une pastille piézoélectrique : la contrainte appliquée crée un signal électrique. La piézoélectricité (du grec piézein presser, appuyer) est la propriété que possèdent certains corps de se… …   Wikipédia en Français

  • Piezzoélectricité — Piézoélectricité Illustration du comportement d’une pastille piézoélectrique : la contrainte appliquée crée un signal électrique. La piézoélectricité (du grec piézein presser, appuyer) est la propriété que possèdent certains corps de se… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”