2^67-1

2^67-1

147 573 952 589 676 412 927

147 573 952 589 676 412 927 = 267-1 est un nombre de mersenne (M67) qui n'est pas premier. Cela a été démontré en 1903 par Frank Nelson Cole, qui lors d'une réunion de la Société mathématique américaine, inscrivit sur un tableau :

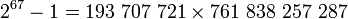2^{67} -1 = 193~707~721 \times 761~838~257~287.

De son propre aveu, Cole a passé pendant trois années tous ses dimanches après-midi à tenter de « casser » ce nombre[1].

Notes

  1. ↑ Marcus du Sautoy, La Symphonie des nombres premiers, ISBN 2-35087-011-1 page 141 ed. Héloïse d'Ormesson (Points)

Liens internes

Grands nombres
Listes de grands nombres Nombres 1000 à 1999 • Nombres 2000 à 2999 • Nombres 3000 à 3999 • Nombres 4000 à 4999 • Nombres 5000 à 5999 • Nombres 6000 à 6999 • Nombres 7000 à 7999 • Nombres 8000 à 8999 • Nombres 9000 à 9999 • Nombres 10 000 à 99 999 • Liste des grands nombres
  • Portail des mathématiques Portail des mathématiques
  • Portail de la cryptologie Portail de la cryptologie
Ce document provient de « 147 573 952 589 676 412 927 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article 2^67-1 de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”