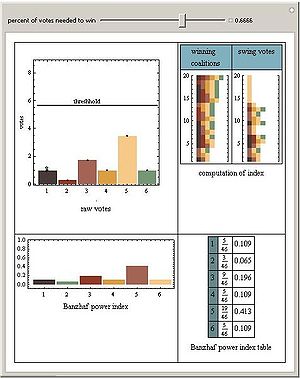
Indice de pouvoir de Banzhaf

Indice de pouvoir de Banzhaf

L’indice de pouvoir de Banzhaf, nommée d'après John F. Banzhaf III, bien qu'à l'origine inventé par Penrose et parfois appelé indice de Penrose-Banzhaf, est un indice de pouvoir défini par la probabilité du changement des résultats d'un scrutin où les droits de vote ne sont pas nécessairement partagés également entre les électeurs[1].

Modélisation informatique de l’indice de pouvoir de Banzhaf.

Pour calculer le pouvoir d'un électeur en utilisant l'indice de Banzhaf, il faut recenser toutes les coalitions gagnantes, puis compter les électeurs critiques : un électeur critique est un électeur qui, s'il a changé son vote de oui en non, entraînerait le rejet de la proposition soumise au vote. Le pouvoir d'un électeur est défini comme la fraction de tous les votes critiques qu'il pouvait exprimer.

L'indice est également connu sous le nom d’indice de Banzhaf-Coleman.

Sommaire

Exemples

Un jeu de vote simple, tiré de Game Theory and Strategy par Phillip D. Straffin:
[6, 4, 3, 2, 1]

Les chiffres entre parenthèses signifient qu’une proposition nécessite 6 voix pour être adoptée, que l’électeur A dispose de quatre voix, l’électeur B de trois voix, l’électeur C de deux voix, et l’électeur D d’une voix. Les groupes gagnants, où ont été surlignés en gras les électeurs décisifs, sont les suivants :
AB, AC, ABC, ABD, ACD, BCD, ABCD

Il y a au total 12 votes décisifs, si bien qu’avec l'indice Banzhaf, le pouvoir est réparti de la manière suivante :
A = \frac{5}{12}, B = \frac{3}{12}, C =\frac{3}{12}, D = \frac{1}{12}

Considérons le collège électoral pour l’élection présidentielle américaine. Chaque État a un nombre de grands électeurs déterminé par l’importance de sa population avec un seuil de voix minimum pour tous les états.
Il y a 538 grands électeurs au total.
La majorité requise pour élire le président est de 270 voix.
L’indice de pouvoir de Banzhaf peut être interprété comme une représentation mathématique de la probabilité qu'a un seul État d’être en mesure de faire basculer le vote.
Un État tel que la Californie, qui dispose de 55 grands électeurs, est plus susceptible de faire basculer le vote qu'un État comme le Montana, qui ne compte que trois grands électeurs[2].

Aux États-Unis, le vote à l’élection présidentielle se fait entre un Républicain et un Démocrate.
Pour simplifier, supposons que seuls trois États y participent : la Californie (55 grands électeurs), Texas (34 grands électeurs), et New York (31 grands électeurs).

Les résultats possibles de l'élection sont les suivants :

Californie (55) Texas (34) New York (31) Votes pour R Votes pour D Etat pouvant faire basculer le vote
R R R 120 0 aucun
R R D 89 31 Californie (D gagnerait par 86 contre 34) et Texas (D gagnerait par 65 contre 55)
R D R 86 34 Californie (D gagnerait par 89 contre 31) et New York (D gagnerait par 65 contre 55)
R D D 55 65 Texas (R gagnerait par 89 contre 31) et New York (R gagnerait par 86 et 34)
D R R 65 55 Texas (D gagnerait par 89 contre 31) et New York (D gagnerait par 86 contre 34)
D R D 34 86 Californie (R gagnerait par 89 contre 31) et New York (R gagnerait par 65 contre 55)
D D R 31 89 Californie (R gagnerait par 86 contre 34) et Texas (R gagnerait par 65 contre 55)
D D D 0 120 Aucun


L’indice de pouvoir de Banzhaf d'un État est la proportion des résultats possibles dans lequel cet État peut faire basculer l'élection.
Dans cet exemple, les trois États ont le même indice : 4 / 12 ou 1 / 3.

Toutefois, si New York est remplacé par l'Ohio, avec seulement 20 grands électeurs, la situation change radicalement :

Californie (55) Texas (34) Ohio (20) Votes pour R Votes pour D Etat pouvant faire basculer le vote
R R R 109 0 Californie (D gagnerait par 55 contre 54)
R R D 89 20 Californie (D gagnerait par 75 contre 34)
R D R 75 34 Californie (D gagnerait par 89 contre 20)
R D D 55 54 Californie (D gagnerait par 109 contre 0)
D R R 54 55 Californie (R gagnerait par 109 contre 0)
D R D 34 75 Californie (R gagnerait par 89 contre 20)
D D R 20 89 Californie (R gagnerait par 75 contre 34)
D D D 0 109 Californie (R gagnerait par 55 contre 54)


Dans cet exemple, l'indice de Banzhaf donne à la Californie 1 et aux autres États 0, puisque la Californie à elle seule dispose de plus de la moitié des voix.

Écriture mathématique

Indice de Banzhaf : Pour un jeu (N,v) l'indice de Banzhaf du joueur i est :

Bi(v) = \frac{di(v)}{\sum_{j\in S\geq N} dj(v)}


où di(v) est l'ensemble des coalitions pour lesquelles i est décisif.

Histoire

Ce qui est connu aujourd'hui comme l'indice de pouvoir de Banzhaf a été initialement présenté par Penrose en 1946 et fut en grande partie oublié par la suite. Il a été réinventée par Banzhaf en 1965, mais il dû être réinventer une fois de plus par Coleman en 1971 avant qu'il soit incorporé à la littérature traditionnelle[3].

Banzhaf voulait prouver objectivement que le système de vote au Conseil du Comté de Nassau était injuste. Comme cela est indiqué dans Game Theory and Strategy, les votes étaient répartis comme suit :

  • Hempstead 1: 9
  • Hempstead 2: 9
  • North Hempstead: 7
  • Oyster Bay: 3
  • Glen Cove: 1
  • Long Beach: 1

On a au total 30 voix, et une majorité simple de 16 voix était nécessaire pour qu'une mesure puisse passer.
En utilisant la notation de Banzhaf, [Hempstead 1, Hempstead 2, North Hempstead, Oyster Bay, Glen Cove, Long Beach] sont notés de A à F et on a le système de poids suivant :
[16, 9, 9, 7, 3, 1, 1]

Il y a 32 coalitions gagnantes, et 48 votes décisifs :
AB, AC, BC, ABC, ABD, ABE, ABF, ACD, ACE, ACF, BCD, BCE, BCF, ABCD, ABCE, ABCF, ABDE, ABDF, ABEF, ACDE, ACDF, ACEF, BCDE, BCDF, BCEF, ABCDE, ABCDF, ABCEF, ABDEF, ACDEF, BCDEF et ABCDEF

L'indice de Banzhaf donne les valeurs de pouvoirs suivantes :

  • Hempstead 1 = 16/48
  • Hempstead 2 = 16/48
  • North Hempstead = 16/48
  • Oyster Bay = 0 / 48
  • Glen Cove = 0 / 48
  • Long Beach = 0 / 48

Banzhaf a fait valoir qu'une convention de vote qui donne 0% du pouvoir à 16% de la population est injuste, et a poursuivi le Conseil en Justice.
Aujourd'hui, l'indice de pouvoir de Banzhaf est un moyen accepté pour mesurer le pouvoir d’un vote, en alternance avec l’indice de pouvoir de Shapley-Shubik. Cependant, l'analyse de Banzhaf a été critiquée pour traiter les voix, comme des pièces de monnaie se retournant, et un modèle empirique de vote plutôt qu’un modèle de vote aléatoire tel qu'il est utilisé par Banzhaf apporte des résultats différents (Gelman & Katz 2002).

Liens internes

Notes et références

  1. ↑ Banzhaf, John F. (1965), Weighted voting doesn't work: A mathematical analysis, Rutgers Law Review 19 (2): 317–343
  2. ↑ Felsenthal, Dan S; Machover, Moshé (1998), The measurement of voting power theory and practice, problems and paradoxes, Cheltenham: Edward Elgar
  3. ↑ Coleman, James S. (1971), Control of Collectives and the Power of a Collectivity to Act, in Lieberman, Bernhardt, Social Choice, New York : Gordon and Breach, pp. 192–225

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Indice de pouvoir de Banzhaf de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Indice de pouvoir de Shapley-Shubik — L’indice de pouvoir de Shapley Shubik a été formulé par Lloyd Shapley et Martin Shubik en 1954[1] pour mesurer le pouvoirs de joueurs dans un jeu de vote. L indice révèle souvent une distribution surprenante du pouvoir qui n est pas évidente au… …   Wikipédia en Français

  • Indices de pouvoir — Un indice de pouvoir est un outil utilisé en politique microéconomique, une branche de l économie, qui a été développé en premier par Lloyd Shapley et Martin Shubik en 1954 pour mesurer le pouvoir des participants à un jeu de vote suivant l… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Valeur de Shapley — En théorie des jeux, la valeur de Shapley permet une répartition équitable des gains dans un jeu coopératif. Sommaire 1 Introduction 2 La solution de Shapley 3 Exemple …   Wikipédia en Français

  • Lloyd Shapley — Lloyd S. Shapley Photo de Lloyd S. Shapley en 1980 Naissance 2 juin 1923 Cambridge (États Unis) Nationalité Américain …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”