¬

Pour les articles homonymes, voir Négation.

En logique et en mathématiques, la négation est un opérateur logique unaire, on dit aussi connecteur logique. Il sert à créer une proposition à partir d'une autre en en inversant la signification, de « vrai » en « faux » ou de « démontrable » en « non démontrable ».

La négation d'une proposition P peut s'écrire de diverses manières :

• ¬P;
• Non P;
• ~P;

et ces formulations se lisent « négation de P » ou plus simplement « non P ».

Dans l'interprétation par des tables de vérité, la proposition ¬P est vraie quand P est fausse et elle est fausse quand P est vraie. La table de vérité s'écrit simplement :

En logique classique, la double négation correspond à une affirmation; autrement dit, les propositions P et ¬ (¬P) sont logiquement équivalentes. En logique intuitionniste, la proposition ¬¬P est plus faible que P, dans le sens où P implique ¬¬P, mais ¬¬P n'implique pas P. Néanmoins, les propositions ¬¬¬P et ¬P sont logiquement équivalentes.

Voici quelques règles d'utilisation des négations en logique classique :

"Non (P ou Q)" équivaut à "(Non P) et (Non Q)"

"Non (P et Q)" équivaut à "(Non P) ou (Non Q)"

"Non (P 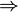Q)" équivaut à "P et (Non Q)"

"Non ( x, P(x))" équivaut à "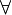 x, Non P(x)"

"Non ( 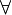x, P(x))" équivaut à " x, Non P(x)"

• Portail de la logique
• Portail des mathématiques