Vortex Street de Kármán

Vortex Street de Kármán

Allée de tourbillons de Karman

allée de tourbillons de Karman au large de l'île Rishiri au Japon.
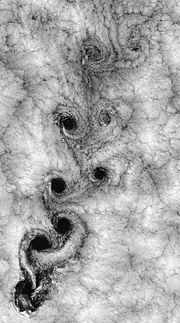Allée de tourbillon de Karman dans les nuages provoquée par la rencontre entre du vent et l'île de Juan Fernandez

Une allée de tourbillons de Karman, ou allée de Bénard-Von Karman (vortex street en anglais) est un motif périodique de tourbillons causés par la séparation instable d'un écoulement autour de corps peu profilés. Une allée de tourbillons ne peut s'observer qu'à l'intérieur d'un intervalle donné de nombres de Reynolds, généralement entre un système de tourbillons attaché à l'obstacle et la turbulence.

Sommaire

Description

Lorsqu'un tourbillon se détache, un écoulement dissymétrique se forme autour du corps, ce qui modifie la distribution des pressions. Cela signifie que la séparation alternée des tourbillons peut créer sur ce corps une portance périodique, cause de vibrations. Si la fréquence de séparation est voisine de la fréquence propre d'une structure, cela crée une résonance. C'est cette vibration forcée qui, à la fréquence correcte, fait «chanter» les lignes électriques ou celles de téléphone, augmente à certaines vitesses les vibrations des antennes des voitures et est également responsable des battements des stores vénitiens quand le vent passe à travers. Dans divers problèmes techniques, ce phénomène peut avoir des conséquences beaucoup plus dommageables (rupture de ponts suspendus, écroulement de cheminées,...).

Fréquence de détachement

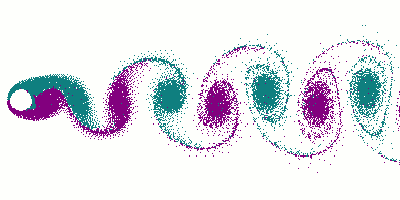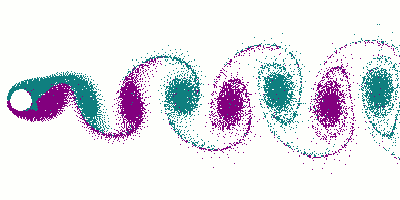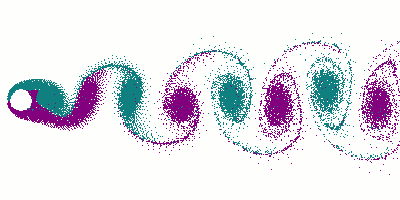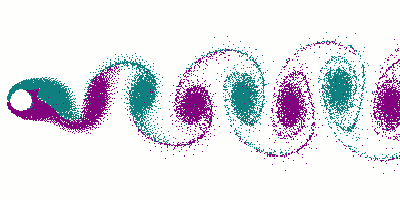Animation du phénomène
Crédits : Cesareo de La Rosa Siqueira

L'expérience montre que la fréquence f de détachement des tourbillons dépend essentiellement des grandeurs suivantes :

Selon la méthode décrite dans Nombre sans dimension, on peut alors calculer la fréquence en fonction des autres variables selon une formule qui doit s'écrire :

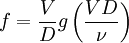
f = {V \over D} g\left(\frac{V D}{\nu}\right)

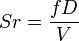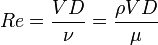En réécrivant la formule, on voit que le nombre de Strouhal Sr = \frac{fD}{V} est fonction du nombre de Reynolds Re = \frac{V D}{\nu} = \frac{\rho V D}{\mu}.

Pour un cylindre à section circulaire, l'expérience montre que cette fonction est, avec une bonne approximation, constante et égale à 0,2.

Cas des insectes

Des études récentes démontrent que certains insectes tirent de l'énergie des vortex qui se forment autour de leurs ailes en vol. Habituellement, un vortex ne peut créer que de la traînée. Ces insectes peuvent recapturer de cette énergie pour améliorer leur vitesse et leur manœuvrabilité. Ils effectuent une rotation avec leurs ailes avant le battement de retour pour que leurs ailes soient levées par le tourbillon (eddy ou vortex, en anglais) d'air créé par le battement vers le bas.

Notes et références

Voir aussi

Commons-logo.svg

Article connexe

Lien externe

  • Portail de la physique Portail de la physique
  • Portail de la météorologie Portail de la météorologie
  • Portail de l’aéronautique Portail de l’aéronautique
Ce document provient de « All%C3%A9e de tourbillons de Karman ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Vortex Street de Kármán de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Karman vortex street — /kärˈmən vörˈteks strēt/ (acoustics) noun The regular vortex pattern behind an obstacle in a flow where vortices are generated and travel away from the object ORIGIN: T von Karman (1881–1963), Hungarian born American engineer …   Useful english dictionary

  • Kármán vortex street — A Kármán vortex street is a repeating pattern of swirling vortices caused by the unsteady separation of flow over bluff bodies. They are named after the engineer and fluid dynamicist, Theodore von Kármán [Theodore von Kármán: Aerodynamics]… …   Wikipedia

  • Karman vortex street — Karmano sūkurių grandinėlė statusas T sritis fizika atitikmenys: angl. Karman vortex path; Karman vortex street vok. Karmansche Wirbelstraße, f; Karman Wirbel, m rus. вихревая дорожка, f; вихревая дорожка Кармана, f; вихревые цепочки Кармана, f;… …   Fizikos terminų žodynas

  • Kármán vortex street — noun A Von Kármán vortex street …   Wiktionary

  • Von Kármán vortex street — noun a double row of vortices in a fluid sometimes found in the wake of a cylindrical body (such as in a river, downstream of a bridge support), eddies being produced from alternate sides of the body Syn: Kármán vortex street …   Wiktionary

  • Vortex shedding — is an unsteady flow that takes place in special flow velocities (according to the size and shape of the cylindrical body). In this flow, vortices are created at the back of the body and detach periodically from either side of the body. See Von… …   Wikipedia

  • Vortex induced vibration — Vortex induced vibrations (VIV) are motions induced on bodies facing an external flow by periodical irregularities on this flow. The classical example is the VIV of an underwater cylinder. You can see how this happens by putting a cylinder into… …   Wikipedia

  • Karman vortex path — Karmano sūkurių grandinėlė statusas T sritis fizika atitikmenys: angl. Karman vortex path; Karman vortex street vok. Karmansche Wirbelstraße, f; Karman Wirbel, m rus. вихревая дорожка, f; вихревая дорожка Кармана, f; вихревые цепочки Кармана, f;… …   Fizikos terminų žodynas

  • Karman-Wirbel — Karmano sūkurių grandinėlė statusas T sritis fizika atitikmenys: angl. Karman vortex path; Karman vortex street vok. Karmansche Wirbelstraße, f; Karman Wirbel, m rus. вихревая дорожка, f; вихревая дорожка Кармана, f; вихревые цепочки Кармана, f;… …   Fizikos terminų žodynas

  • Kármán, Theodore von — born , May 11, 1881, Budapest died May 6, 1963, Aachen, W.Ger. Hungarian born U.S. engineer. After directing the Aeronautical Institute at Aachen, Germany (1912–30), he immigrated to the U.S., where he taught at the California Institute of… …   Universalium

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”