Viscosite des solutions polymeres

Viscosite des solutions polymeres

Viscosité des solutions polymères

La dissolution d'un polymère dans un solvant (lorsqu'une telle dissolution est possible) augmente la viscosité de la solution. A partir de mesures de la viscosité de la solution pour différentes concentrations en polymère dissous, on peut calculer la masse molaire moyenne viscosimétrique. Elle est notée 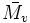\bar{M_v}. Contrairement aux autres masses molaires moyennes, 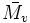\bar{M_v} n'est pas une valeur absolue car elle dépend du solvant utilisé et de la température.

Sommaire

Différentes définitions

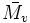Il nous faut introduire certaines notations avant de présenter brièvement l'architecture théorique permettant au final de déterminer \bar{M_v}.

Notations : viscosité des solutions polymères

Introduisons tout d'abord les notations suivantes : soit η la viscosité du solvant en l'absence de polymère dissous. Soit η0(c) la viscosité de la solution contenant une concentration c de polymère dissous.

  • Viscosité relative : c'est un nombre sans dimension représentant le rapport de la visosité de la solution sur la viscosité du solvant :

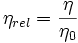
\eta_{rel} = \frac{\eta}{\eta_0}

  • Viscosité spécifique : (également sans dimension)

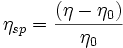
\eta_{sp} = \frac{(\eta-\eta_0)}{\eta_0}

  • Viscosité réduite : il s'agit du rapport de la viscosité spécifique sur la concentration en polymère dissous. La viscosité réduite a donc la dimension de l'inverse d'une concentration[1].

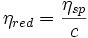
\eta_{red} = \frac{\eta_{sp}}{c}

  • Viscosité intrinsèque : notée [η], il s'agit de la limite de la viscosité spécifique lorsque la concentration en polymère dissous tend vers zéro. La viscosité intrinsèque a également la dimension de l'inverse d'une concentration.

[\eta] = \lim_{c \to 0}\left(\frac{\eta_{sp}}{c}\right)

  • Viscosité inhérente : (dimension de l'inverse d'une concentration)

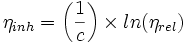
\eta_{inh} = \left(\frac{1}{c}\right) \times ln (\eta_{rel})

Les relations entre ces grandeurs

Mesurer la viscosité intrinsèque

Résolution mathématique

Méthodes de résolution graphique

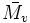
Obtenir \bar{M_v}

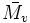La loi de Mark-Houwink-Sakurada (MHS) permet de relier la viscosité intrinsèque [η] à la masse molaire moyenne viscosimétrique \bar{M_v}.

[\eta] = K \times M^{\alpha}

Il s'agit d'une relation semi-empirique. Les coefficients K et α varient avec le couple (solvant/polymère) considéré et la température de la solution. Il existent des tables donnant les valeurs de ces coefficients en fonction de ces paramètres.

La relation MHS peut être reécrite sous la forme suivante en prenant le logarithme de chacun de ces termes :

ln\, ([\eta]) = ln\, (K) + \alpha \times ln\,(M)

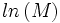Cette relation linéaire permet de déterminer aisément les valeurs des coefficients α et K. Si l'on représente ln\, ([\eta]) en fonction de ln\,(M), on devrait obtenir une droite de pente α et d'ordonnée à l'origine ln(K).

Remarque : lorsque α = 1, on parle également de relation de Staudinger

Notes

  1. ↑ Par exemple : des L.kg-1 avec les unités SI.
  • Portail de la chimie Portail de la chimie
Ce document provient de « Viscosit%C3%A9 des solutions polym%C3%A8res ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Viscosite des solutions polymeres de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Viscosité des solutions polymères — La dissolution d un polymère dans un solvant (lorsqu une telle dissolution est possible) augmente la viscosité de la solution. À partir de mesures de la viscosité de la solution pour différentes concentrations en polymère dissous, on peut… …   Wikipédia en Français

  • Viscosité — La substance du dessus a une viscosité moindre que celle du dessous La viscosité (du latin viscum, gui) peut être définie comme la résistance à l écoulement uniforme et sans turbulence se produisant dans la masse d une matière. La viscosité… …   Wikipédia en Français

  • POLYMÈRES - Théorie sur les polymères — Nous nous limiterons ici à l’essentiel des théories actuelles sur les polymères. Nous ne traiterons pas des problèmes de préparation des polymères et des techniques d’études classiques, nous n’étudierons pas non plus les nombreuses applications… …   Encyclopédie Universelle

  • RÉSISTANCE DES MATÉRIAUX — La résistance des matériaux est la science du dimensionnement. Concevoir une pièce mécanique, un ouvrage d’art ou tout objet utilitaire, c’est d’abord imaginer les formes et le squelette géométrique qui remplissent les fonctions demandées; c’est… …   Encyclopédie Universelle

  • Polymère en solution — Comprendre le comportement des polymères en solution est important pour certaines applications comme les gels et crèmes cosmétiques. Il y a possibilité de contrôler la viscosité du produit obtenu et d éviter une éventuelle démixtion (séparation… …   Wikipédia en Français

  • PÉTROLE - L’exploitation des gisements — S’il incombe aux équipes de prospection de trouver des gisements, le rôle de celles qui sont chargées de la production est d’en tirer le meilleur parti. Essentiellement empirique d’abord, l’extraction des hydrocarbures, pétrole et gaz naturel,… …   Encyclopédie Universelle

  • MACROMOLÉCULES — Les macromolécules sont des systèmes moléculaires constitués par un très grand nombre d’atomes assemblés entre eux par des liaisons covalentes. Alors que les molécules simples sont formées de quelques dizaines d’atomes au maximum, les… …   Encyclopédie Universelle

  • COLLOÏDES — Les solutions colloïdales ou sols sont constituées par un liquide dans lequel un corps, généralement solide, est dispersé en granules dont la dimension moyenne est comprise entre deux dixièmes et deux millièmes de micromètres. Ces granules sont… …   Encyclopédie Universelle

  • GLUCIDES — Les glucides, les lipides et les protides sont les trois grandes familles de composés naturels dont le rôle biologique est fondamental. Glucides est le nom moderne de ce que l’on appelait autrefois «saccharides». En fait, les glucides comprennent …   Encyclopédie Universelle

  • CHROMATOGRAPHIE — La chromatographie est une méthode d’analyse chimique consistant à séparer les constituants d’un mélange. Aussi est elle universellement employée, au laboratoire comme dans l’industrie, tant pour l’analyse proprement dite que pour la séparation… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”