- Vaisseau (automate cellulaire)
-
Pour les articles homonymes, voir vaisseau.
Dans un automate cellulaire, un motif fini est nommé vaisseau, ou navire, s'il réapparait au bout d'un certain nombre de générations dans une position différente. Un vaisseau ressemble à un puffeur, à ceci près que contrairement à ce dernier, un vaisseau n'émet par définition pas de débris. Aussi, on peut transformer un puffeur en vaisseau en arrivant à détruire ses débris comme pour l'écologiste.
Le concept de vaisseau a été introduit par John Horton Conway pour le Jeu de la vie — sous le nom anglais de spaceship, vaisseau spatial[1]. Bien que cette notion s'applique a priori à n'importe quel automate cellulaire, elle a été surtout étudiée dans le Jeu de la vie, qui en a sans doute produit les spécimens les plus spectaculaires et les plus nombreux.
Sommaire
Vitesse
En premier lieu, le nombre minimum de générations nécessaires à la réplication du motif en un autre endroit est nommé la période du vaisseau.
Pour un automate cellulaire, il existe une vitesse maximale à laquelle un effet peut se propager et qui dépend des règles utilisées (par exemple, pour le Jeu de la vie qui ne prend en compte pour la génération suivante d'une cellule que celles qui lui sont strictement adjacentes, cette vitesse maximale est d'une cellule par génération). Historiquement, Conway a nommé cette vitesse la « vitesse de la lumière », et l'a notée c — par analogie à la vitesse de la lumière du monde physique, théoriquement indépassable.
Pour un automate cellulaire à deux dimensions, si un vaisseau se déplace de A cases horizontalement et de B cases verticalement sur N générations (on peut d'ailleurs montrer que
), on définit sa vitesse comme égale à 
. Par exemple, une vitesse de 
signifie que le vaisseau se déplace d'une cellule (horizontalement, verticalement, ou les deux en même temps) toutes les quatre générations.Exemples
Dès les débuts du Jeu de la vie en 1970, quatre vaisseaux furent découverts car ils apparaissent relativement spontanément dans beaucoup de configurations :
Image Nom Commentaire fixe en déplacement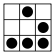 
Le planeur C'est le plus petit vaisseau du jeu de la vie : cinq cellules contenues dans un carré de trois cellules sur trois. Il se déplace d'une case en diagonale toutes les quatre générations, pour une vitesse de C/4. 
LWSS Trois autres vaisseaux se déplacent horizontalement (ou verticalement) de deux cases toutes les quatre générations, pour une vitesse de C/2. Ils portent en anglais le nom de Light, Medium et Heavy Weight Spaceships (littéralement « vaisseaux de poids léger, moyen et lourd »), généralement abrégés en LWSS, MWSS et HWSS. 
HWSS en mouvement
Le HWSS Le HWSS est le pus gros vaisseau de la famille du LWSS. Depuis, de nombreux autres vaisseaux furent découverts, se déplaçant éventuellement à des vitesses différentes.
Structures associées
Réflecteurs
Un motif qui, lorsqu'il est atteint par un vaisseau, produit une copie de ce vaisseau se déplaçant dans un direction différente est appelée un réflecteur.
Tagalongs et pushalongs
Un tagalong (terme anglais signifiant à peu-près « suiveur ») est un motif qui n'est pas un vaisseau par lui-même, mais qui peut être attaché derrière un vaisseau pour en former un plus grand. Souvent, plusieurs tagalongs peuvent être attachés successivement, pouvant même rattacher plusieurs vaisseaux distincts.
Apparenté au tagalong, le pushalong (terme anglais qui signifie à peu près pousseur) est un motif qui n'est pas un vaisseau par lui-même, mais qui peut être attaché devant un vaisseau pour en former un plus grand.
-
Un exemple de tagalong trouvé par Paul Schick en 1972. Notez qu'il est attaché à deux LWSS.
-
Un exemple de pushalong avec un MWSS. Il a été trouvé par David Bell en 1992.
OWSS et flottilles
Un OWSS est un vaisseau du type LWSS plus long que le HWSS. Or, le OWSS est trop gros pour exister car l'un de ses sparks (étincelles ou débris en français) est une ligne de 3 ou plus. Ces lignes ne disparaissent pas (ou du moins, pas à temps) et détruisent le OWSS. Il existe cependant un moyen pour stabiliser le OWSS: on peut empêcher ce débris d'exister avec deux vaisseaux plus petits (si ces vaisseaux sont eux-mêmes des OWSS, on peut les stabiliser avec des vaisseaux encore plus petits). Le OWSS devient alors un tagalong et crée un vaisseau en forme de double triangle appelé flottille
Une flottille où un OWSS (au centre) est escorté par deux HWSS.Information
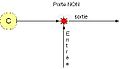
Les vaisseaux peuvent aussi être utilisés pour transmettre de l'information. Par exemple, dans le Jeu de la vie, le planeur peut servir à cette fonction. Il existe des Portes logiques pour planeurs[2].
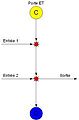
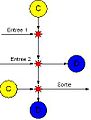
Dans les trois schémas qui suivent, une flèche est une file de planeurs, un cercle bleu indique que la file arrivant est détruite, un cercle jaune est un canon à planeurs, un cercle vert indique que la file rebondit(et la file arrivant est donc la même que celle sortant) et une étoile rouge indique que les deux files arrivant s'annihilent. Ces images ont été basculées à 45° pour être plus claires.
-
Une porte NON.
-
Une porte ET.
-
Une porte OU.
-
Une porte OU EXCLUSIF (XOR). On peut obtenir une porte ÉGAL en plaçant une porte NON juste après.
Annexes
Articles connexes
Liens externes
- (en) Spaceships in Conway's Game of Life : copie d'une série de messages postés par David L. Bell sur le groupe comp.theory.cell-automata en 1992, faisant le tour de l'état de l'art de l'époque
- (en) Gliders in Life-Like Cellular Automata : compilation de vaisseaux dans divers automates cellulaires
- (en) The 17c/45 Caterpillar spaceship : un vaisseau construit à partir de blocs séparés, de période 17c/45, en 2004. Haut de 330 721 cellules, large de 4 195 et comptant à peu près 12 millions de cellules, il s'agit à l'heure actuelle du plus grand objet jamais créé pour le Jeu de la vie
- (en) Paul's page of Conways Life Miscellany : de nombreuses figures du jeu de la vie avec leur code
- Cornway's game of life : un site avec un excellent éditeur de figures de la vie, et des constructions à regarder évoluer.
Bibliographie
- Martin Gardner, Mathematical Games. The fantastic combinations of John Conway's new solitaire game "life", Scientific American n°223 (Octobre 1970), p. 120-123
- William Poundstone, The recursive universe, Cosmic Complexity and the Limits of Scientific Knowledge, Oxford University Press (1987), p.78-89
Référence
- Martin Gardner, Mathematical Games. The fantastic combinations of John Conway's new solitaire game "life", Scientific American n°223 (Octobre 1970), p. 120-123
- William Poundstone, The recursive universe, Cosmic Complexity and the Limits of Scientific Knowledge, Oxford University Press (1987), p.78-89
-
Wikimedia Foundation. 2010.
