B-Arbre

Un arbre B (appelé aussi B-arbre par analogie au terme anglais « B-tree ») est un arbre équilibré qui est principalement mis en œuvre dans les mécanismes de gestion de bases de données et de systèmes de fichiers. Il stocke les données sous une forme triée et permet une exécution des opérations d'insertion et de suppression en temps amorti logarithmique.

Le principe général est de permettre aux nœuds de posséder plus d'une clé ; cela minimise la taille de l'arbre et réduit le nombre opérations d'équilibrage. De plus un B-arbre grandit à partir de la racine, contrairement à un arbre binaire de recherche qui pousse à partir des feuilles.

Le créateur des arbres B, Rudolf Bayer, n'a pas explicité la signification du "B". L'explication la plus fréquente est que le B correspond au terme anglais "balanced" (en français : équilibré). Cependant il pourrait aussi découler de "Bayer", du nom du créateur, ou de "Boeing", du nom de la firme pour laquelle le créateur travaillait (Boeing Scientific Research Labs).

Sommaire 1 Structure 2 Opérations 2.1 Recherche 2.2 Insertion 2.3 Suppression 3 Remarques 4 Variantes 5 Annexes 5.1 Bibliographie 5.2 Notes et références 6 Voir aussi 6.1 Articles connexes 6.2 Liens externes

Structure

Soient L et U deux entiers naturels non nuls tels que L ≤ U. On définit alors un L-U arbre B^[1] de la manière suivante : chaque nœud sauf la racine possède au moins L−1 clés (appelées aussi éléments), au plus U−1 clés et au plus U fils^[2]. Pour chaque nœud interne – nœud qui n’est pas une feuille –, le nombre de fils est toujours égal au nombre de clés augmenté d’une unité. Si n est le nombre de fils, alors on parle de n-nœud. Un L-U arbre ne contient que des n-nœuds avec L ≤ n ≤ U. Souvent on choisit la configuration L = t et U = 2 × t : t est appelé le degré minimal de l’arbre B.

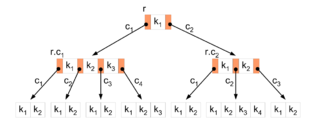
De plus la construction des arbres B implique qu’un arbre B est toujours équilibré. Chaque clé d’un nœud interne est en fait une borne qui distingue les sous-arbres de ce nœud. Par exemple, si un nœud a 3 fils – lesquels constituent les racines respectives de trois sous-arbres : sous-arbre gauche, sous-arbre du milieu et sous-arbre droit –, alors il a 2 clés notées c₁ et c₂ qui délimitent les clés de chaque sous-arbre : les clés du sous-arbre gauche seront inférieures à c₁ ; les clés du sous-arbre du milieu seront comprises entre c₁ et c₂ ; les clés du sous-arbre droit seront supérieures à c₂.

Opérations

Recherche

La recherche est effectuée de la même manière que dans un arbre binaire de recherche. Partant de la racine, on parcourt récursivement l’arbre ; à chaque nœud, on choisit le sous-arbre fils dont les clés sont comprises entre les mêmes bornes que celles de la clé recherchée.

Insertion

L’insertion nécessite tout d’abord de chercher le nœud où la nouvelle clé devrait être insérée, et l’insérer. La suite se déroule récursivement, selon qu’un nœud ait ou non trop de clés : s’il possède un nombre acceptable de clés, on ne fait rien ; autrement on le transforme en deux nœuds, chacun possédant un nombre minimum de clés, puis on fait « remonter » la clé du milieu qui est alors insérée dans le nœud père. Ce dernier peut du coup se retrouver avec un nombre excessif de fils ; le procédé se poursuit ainsi jusqu’à ce que l’on atteigne la racine. Si celle-ci doit être divisée, on fait « remonter » la clé du milieu dans une nouvelle racine, laquelle génèrera comme nœuds fils les deux nœuds créés à partir de l’ancienne racine, à l’instar de l'étape précédente. Pour que l’opération soit possible, on remarque qu’il faut que U ≥ 2 L ; sinon les nouveaux nœuds ne possèderont pas suffisamment de clés.

Une variante consiste à éclater préventivement chaque nœud « plein » (possédant le nombre maximal de clés) rencontré lors de la recherche du nœud où se réalisera l'insertion. De cette manière on évite une remontée dans l'arbre, puisque l'on assure que le père d'un nœud à scinder en deux peut accueillir une clé supplémentaire. La contrepartie en est un légère augmentation de la hauteur moyenne de l'arbre.

Suppression

On doit d’abord chercher la clé à supprimer, et la supprimer du nœud qui la contient.

• Si le nœud est interne, on procède de manière similaire aux arbres binaires de recherche en recherchant la clé k la plus à gauche dans le sous-arbre droit de la clé à supprimer ou la plus à droite dans le sous-arbre gauche. Cette clé k appartient à une feuille. On peut la permuter avec la clé à supprimer, que l’on supprime ensuite. Comme elle appartient à une feuille, on se ramène au cas suivant.
• Si le nœud est une feuille, soit il possède encore suffisamment de clés et l’algorithme termine, soit il dispose de moins de L−1 clés et on se trouve dans l’une des deux situations suivantes :
  • soit un de ses frères à droite ou à gauche possède suffisamment de clés pour pouvoir en "passer" une à la feuille en question : dans ce cas cette clé remplace la clé qui sépare les deux sous-arbres dans l’arbre père, qui va elle même dans la feuille en question ;
  • soit aucun de ses frères n’a suffisamment de clés : dans ce cas, le père fait passer une de ses clés dans un des deux (ou le seul) frères pour permettre à la feuille de fusionner avec celui-ci. Ceci peut cependant conduire le père à ne plus avoir suffisamment de clés. On réitère alors l’algorithme : si le nœud a un frère avec suffisamment de clés, la clé la plus proche va être échangée avec la clé du père, puis la clé du père et ses nouveaux descendants sont ramenés dans le nœud qui a besoin d’une clé ; sinon on effectue une fusion à l’aide d’une clé du père et ainsi de suite. Si l’on arrive à la racine et qu’elle possède moins de L éléments, on fusionne ses deux fils pour donner une nouvelle racine.

Remarques

• La plupart du temps, la configuration est telle que U = 2 L. On parle alors d’arbre B d'ordre L.
• Les arbres 2-3-4 sont les structures de données d’arbre B les plus utilisées : ils correspondent en fait à des 2-4 arbres B ou arbres B d’ordre 2.

Variantes

L’arbre B+ diffère légèrement de l’arbre B, en ceci que toutes les données sont stockées exclusivement dans des feuilles. D’autres variantes existent également, telles que l’arbre B*.

Annexes

Bibliographie

• (en) Rudolf Bayer, Binary B-Trees for Virtual Memory, ACM-SIGFIDET Workshop 1971, San Diego, California, Session 5B, p. 219-235.
• (en) Rudolf Bayer et McCreight, E. M. Organization and Maintenance of Large Ordered Indexes. Acta Informatica 1, 173-189, 1972.

Notes et références

Voir aussi

Articles connexes

• Arbre de fouille

Liens externes

• (en) Slady.net : animation sous forme d’applet Java permettant de construire visuellement des arbres B.
• (it)(en)B-tree GUI : Spataro Fabrizio e Todaro Michelangelo – Emulatore Java BTree – BTree Java Emulator.

• Portail de l’informatique