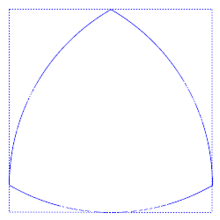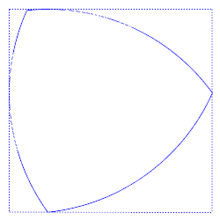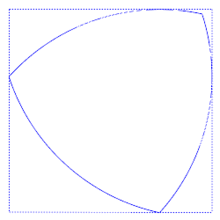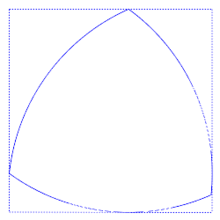
Triangle de Reuleaux

Triangle de Reuleaux
Triangle de Reuleaux

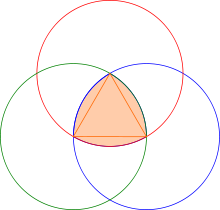
Un triangle de Reuleaux est une courbe de largeur constante, c'est-à-dire une courbe dont tous les diamètres ont même longueur. Elle tient son nom de l'ingénieur allemand Franz Reuleaux, qui fut au XIXe siècle un pionnier du génie mécanique.

Construction d'un triangle de Reuleaux

Sommaire

Construction

Pour construire le triangle de Reuleaux, on part d'un triangle équilatéral. Depuis chaque sommet pris tour à tour, on décrit un arc de cercle entre les deux autres sommets. Les trois arcs raccordés forment un triangle de Reuleaux.

Caractéristiques

Un théorème dû à Henri Léon Lebesgue et Wilhelm Blaschke (1885-1962) établit que cette courbe possède, parmi les courbes d'égale largeur, une surface minimale.

On peut généraliser la construction de Reuleaux aux polygones ayant un nombre de côtés impair : on obtient ainsi des polygones curvilignes de largeur constante, les polygones de Reuleaux.

Comme tous les diamètres ont même longueur, le triangle de Reuleaux – et en fait, tout polygone de Reuleaux – répond à la question suivante : « Quelle forme doit avoir une plaque d'égout pour ne pas tomber dans le regard de visite ? » La réponse la plus simple est le cercle, mais le triangle de Reuleaux convient également. La ville de San Francisco par exemple utilise également des triangles de Reuleaux[1].

un triangle de Reuleaux en rotation dans un carré

Utilisations

On associe le triangle de Reuleaux au compresseur rotatif du moteur Wankel. Le rotor de ce moteur est effectivement à la base un triangle de Reuleaux, dont les faces sont creusées pour augmenter la surface de la chambre de combustion.

Un tétraèdre de Reulaux

Tétraèdre de Reuleaux

L'intersection de sphères de rayon commun s, et dont les centres sont au sommet d'un tétraèdre de côté s s'appelle tétraèdre de Reuleaux.

Contrairement à l'intuition, le tétraèdre de Reuleaux n'est pas de largeur constante : le diamètre de ce solide, c'est-à-dire la distance entre deux points situés au milieu de deux arêtes opposées, est supérieure à la distance séparant deux sommets :

\frac ds=\sqrt3-{\sqrt2\over 2}\approx 1{,}0249

Notes et références

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Triangle de Reuleaux de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Triangle de reuleaux — Le triangle de Reuleaux est une courbe de largeur constante, c est à dire une courbe dont tous les diamètres ont même longueur. Elle tient son nom de l ingénieur allemand Franz Reuleaux, qui fut au XIXe& …   Wikipédia en Français

  • Triangle (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Triangle (homonymie) », sur le Wiktionnaire (dictionnaire universel) Le mot « triangle », du …   Wikipédia en Français

  • Reuleaux triangle — A Reuleaux polygon is a curve of constant width that is, a curve in which all diameters are the same length. The best known version is the Reuleaux triangle. Both are named after Franz Reuleaux, a 19th century German engineer who did pioneering… …   Wikipedia

  • Reuleaux tetrahedron — Animation of a Reuleaux tetrahedron, showing also the tetrahedron from which it is formed. Four spheres intersect to form a Reuleaux tetrahedron. The Reuleaux tetrahedron is the inter …   Wikipedia

  • Reuleaux-Dreieck — Das Reuleaux Dreieck ist das einfachste nicht triviale Beispiel eines Gleichdicks: eine Kurve konstanter Breite – als Breite wird hier der Abstand der Punkte einer Seite zur jeweils gegenüberliegenden Ecke bezeichnet. Das Reuleaux Dreieck ist… …   Deutsch Wikipedia

  • Triangle (disambiguation) — A triangle is a geometric shape that has three straight sides. Triangle can also refer to: Mathematics * Spherical triangle * Sierpinski triangle * Pascal s triangle * Triangle wave * Triangle inequality Objects * Triangle (instrument), a musical …   Wikipedia

  • Tétraèdre de Reuleaux — Animation d un tétraèdre de Reuleaux, mettant également en évidence le tétraèdre à partir duquel il est construit. En géométrie, le tétraèdre de Reuleaux est une forme géométrique, analogue du triangle de Reuleaux à trois dimensions. Sommai …   Wikipédia en Français

  • Reuleaux triangle — noun A figure consisting of three circular arcs, each centered on the intersection of the other two …   Wiktionary

  • Franz Reuleaux — (September 30, 1829 ndash; August 20, 1905), was a mechanical engineer and a lecturer of the Berlin Royal Technical Academy, later appointed as the President of the Academy. He was often called the father of kinematics. He was a leader in his… …   Wikipedia

  • Courbe De Largeur Constante — Le triangle de Reuleaux est une courbe de largeur constante. En géométrie, une courbe de largeur constante est une courbe plane fermée dont la largeur, mesurée par la distance entre deux droites parallèles opposées qui lui sont …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”