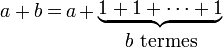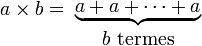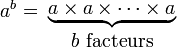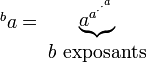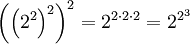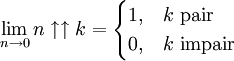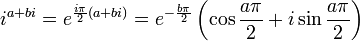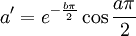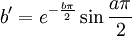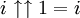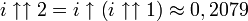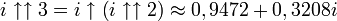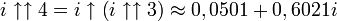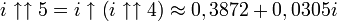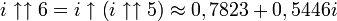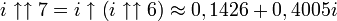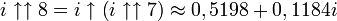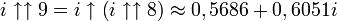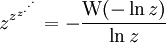Tour de puissance

Tétration

La tétration (ou encore nappe exponentielle, hyperpuissance, tour de puissance, super-exponentiation ou hyper4) est une « exponentiation itérative », le premier hyper opérateur après l'exponentiation. Le mot-valise tétration a été forgé par Reuben Louis Goodstein sur la base du préfixe tétra- (quatre) et itération. La tétration est utilisée pour l'écriture des grands nombres. Elle suit l'addition, la multiplication et l'exponentiation comme indiqué ci-après :

addition

${{a + b} \atop \,} {= \atop \,} {a \, + \atop \, } {{\underbrace{1 + 1 + \cdots + 1}} \atop b \text{ termes}}$
multiplication

${{a \times b = \ } \atop {\ }} {{\underbrace{a + a + \cdots + a}} \atop b\text{ termes}}$
exponentiation

${{a^b = \ } \atop {\ }} {{\underbrace{a \times a \times \cdots \times a}} \atop b\text{ facteurs}}$
tétration

${\ ^{b}a = \ \atop {\ }} {{\underbrace{a^{a^{\cdot^{\cdot^{a}}}}}} \atop b\text{ exposants}}$

chaque opération étant définie par itération à partir de la précédente.

L'addition (a+b) peut être définie comme b itérations de l'opération ajouter 1 appliquée à a, la multiplication (a.b) comme b itérations de l'opération ajouter a appliquée à a, et l'exponentiation ( $a b$ ) comme b itérations de l'opération multiplier par a appliquée à a. De manière analogue, la tétration (^ba) peut être considérée comme b itérations de l'opération porter à la puissance a appliquée à a.

On remarquera que lorsque l'on évalue une exponentiation à niveaux multiples, l'exponentiation est effectuée à un niveau le plus « profond » en premier lieu (en notation, au niveau le plus élevé). En d'autres termes :

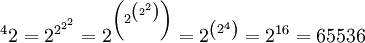
$\,\!\ ^{4}2 = 2^{2^{2^2}} = 2^{\left(2^{\left(2^2\right)}\right)} = 2^{\left(2^4\right)} = 2^{16} = 65536$

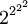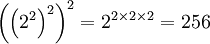$\,\!2^{2^{2^2}}$ n'est pas égal à $\,\! \left({\left(2^2\right)}^2\right)^2 = 2^{2\times2\times2} = 256$ .

Ceci est la règle générale pour l'ordre des opérations impliquant une exponentiation répétée.

Sommaire

1 Notation
2 Exemples
3 Extension aux valeurs faibles du second opérand
4 Tétration complexe
5 Extension aux nombres réels
6 Tours de puissance infiniment hautes
7 Voir aussi
8 Références
9 Liens externes

Notation

Afin de généraliser le premier cas au-dessus (tétration), une nouvelle notation est nécessaire (voir ci-dessous); cependant, le second cas peut-être également écrit :

$\,\! \left(\left(2^2\right)^2\right)^2 = 2^{2 \cdot 2 \cdot 2} = 2^{2^3}$

Donc, sa forme générale utilise toujours une notation d'exponentiation ordinaire.

Les notations dans lesquelles une tétration peut être notée (parmi celles permettant même des niveaux d'itérations plus élevés) incluent :

la notation standard : ^ba, utilisée en premier lieu par Hans Maurer; cette notation a été popularisée le livre de Rudy Rucker, Infinity and the Mind.
la notation des puissances itérées de Knuth : $a \uparrow\uparrow b$ — peut être étendue en utilisant plus de flèches (ou de manière équivalente, une flèche indexée).
la notation des flèches chaînées de Conway : 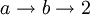$a \rightarrow b \rightarrow 2$ — peut être étendue en augmentant le nombre 2 (équivalentes avec les extensions au-dessus), mais aussi, de manière plus performante, en étendant la chaîne.
la notation hyper4 : 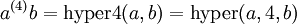$a^{(4)}b = \operatorname{hyper4}(a, b) = \operatorname{hyper}(a, 4, b)$ — peut-être étendue en augmentant le nombre 4; cela donne la famille des hyper opérateurs.

Pour la fonction d'Ackermann, nous avons : 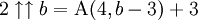$2 \uparrow\uparrow b = \operatorname{A}(4, b - 3) + 3$ , i.e. $\operatorname{A}(4, n) = 2 \uparrow\uparrow (n+3) - 3$ .

La flèche vers le haut est utilisée de manière identique au signe d'omission, ce qui fait que l'opérateur tétration peut être écrit comme ^^ en ASCII : a^^b.

Exemples

(Les exemples avec virgules sont approchées)

n = `n`↑↑1	`n`↑↑2	`n`↑↑3	`n`↑↑4
1	1	1	1
2	4	16	65 536
3	27	7,63×10¹²	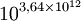$10^{3,64 \times 10^{12}}$
4	256	1,34×10¹⁵⁴	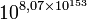$10^{8,07 \times 10^{153}}$
5	3 125	1,91×10^{2 184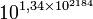}	$10^{1,34 \times 10^{2 184}}$
6	46 656	2,70×10^{36 305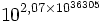}	$10^{2,07 \times 10^{36 305}}$
7	823 543	3,76×10^{695 974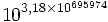}	$10^{3,18 \times 10^{695 974}}$
8	16 777 216	6,01×10^{15 151 335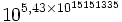}	$10^{5,43 \times 10^{15 151 335}}$
9	387 420 489	4,28×10^{369 693 099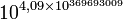}	$10^{4,09 \times 10^{369 693 009}}$
10	10 000 000 000	10^{10 000 000 000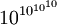}	$10^{10^{10^{10}}}$

Extension aux valeurs faibles du second opérand

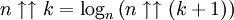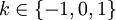En utilisant la relation $n \uparrow\uparrow k = \log_n \left(n \uparrow\uparrow (k+1)\right)$ (déduite de la définition de la tétration), on peut dériver (ou définir) les valeurs pour $n \uparrow\uparrow k$ pour $k \in \{-1, 0, 1\}$ .

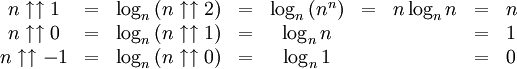
$\begin{matrix} n \uparrow\uparrow 1 & = & \log_n \left(n \uparrow\uparrow 2\right) & = & \log_{n} \left(n^n\right) & = & n \log_{n} n & = & n \\ n \uparrow\uparrow 0 & = & \log_{n} \left(n \uparrow\uparrow 1\right) & = & \log_{n} n & & & = & 1 \\ n \uparrow\uparrow -1 & = & \log_{n} \left(n \uparrow\uparrow 0\right) & = & \log_{n} 1 & & & = & 0 \end{matrix}$

Cela confirme la définition intuitive de $n \uparrow\uparrow 1$ comme étant simplement $n$ . Cependant, on ne peut plus définir plus de valeurs par itération supplémentaire de cette manière, puisque $log n 0$ est indéfini.

De la même manière, puisque $log 11$ est aussi indéfini ( 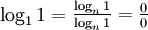$\log_{1} 1 = \begin{matrix}\frac{\log_n 1}{\log_n 1} = \frac{0}{0}\end{matrix}$ ), la dérivation au-dessus ne peut être produite lorsque $n$ = 1. Ainsi, 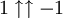$1 \uparrow\uparrow {-1}$ doit rester une quantité non définie, bien que $1 \uparrow\uparrow {0}$ puisse être défini sans problème comme étant égal à 1.

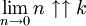Parfois, $00$ est considéré comme quantité indéfinie. Dans ce cas, les valeurs pour $0\uparrow\uparrow{k}$ ne peuvent être définie directement. Cependant, $\lim_{n\rightarrow0} n\uparrow\uparrow{k}$ est bien défini, et existe :

$\lim_{n\rightarrow0} n\uparrow\uparrow k = \begin{cases} 1, & k \mbox{ pair} \\ 0, & k \mbox{ impair} \end{cases}$

Cette limite est également valable pour $n$ négatif. $0 \uparrow\uparrow {k}$ pourrait être définie en termes de cette limite et devrait être en accord avec la définition de $00 = 1$ (si 0 est considéré comme pair).

Tétration complexe

Puisqu'un nombre complexe peut être élevé à la puissance, la tétration peut être appliquée aux nombres de la forme $a + b i$ , dans lesquels $i$ est la racine carrée de -1. Ainsi par exemple, $n \uparrow\uparrow k$ dans lequel $n = i$ , la tétration est effectuée en utilisant la branche principale du logarithme naturel, et on a la relation :

$i^{a+bi} = e^{{i\pi \over 2} (a+bi)} = e^{-{b\pi \over 2}} \left(\cos{a\pi \over 2} + i \sin{a\pi \over 2}\right)$

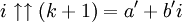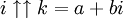Ce qui suggère une définition récursive pour $i \uparrow\uparrow (k+1) = a'+b'i$ pour tout $i \uparrow\uparrow k = a+bi$ :

$a' = e^{-{b\pi \over 2}} \cos{a\pi \over 2}$

$b' = e^{-{b\pi \over 2}} \sin{a\pi \over 2}$

Les valeurs approximées suivantes peuvent en être déduites, pour lesquelles 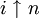$i \uparrow n$ est l'exponentiation ordinaire (i.e. $i n$ ).

$i \uparrow\uparrow 1 = i$
$i \uparrow\uparrow 2 = i \uparrow\left(i \uparrow\uparrow 1\right) \approx 0,2079$
$i \uparrow\uparrow 3 = i \uparrow\left(i \uparrow\uparrow 2\right) \approx 0,9472 + 0,3208i$
$i \uparrow\uparrow 4 = i \uparrow\left(i \uparrow\uparrow 3\right) \approx 0,0501 + 0,6021i$
$i \uparrow\uparrow 5 = i \uparrow\left(i \uparrow\uparrow 4\right) \approx 0,3872 + 0,0305i$
$i \uparrow\uparrow 6 = i \uparrow\left(i \uparrow\uparrow 5\right) \approx 0,7823 + 0,5446i$
$i \uparrow\uparrow 7 = i \uparrow\left(i \uparrow\uparrow 6\right) \approx 0,1426 + 0,4005i$
$i \uparrow\uparrow 8 = i \uparrow\left(i \uparrow\uparrow 7\right) \approx 0,5198 + 0,1184i$
$i \uparrow\uparrow 9 = i \uparrow\left(i \uparrow\uparrow 8\right) \approx 0,5686 + 0,6051i$

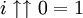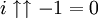La résolution de la relation conduit aux relations attendues $i \uparrow\uparrow 0 = 1$ et $i \uparrow\uparrow -1 = 0$ , avec des valeurs négatives de $k$ donnant des résultats infinis sur les axes imaginaires. Dans le plan complexe, la séquence entière converge en spirale vers la limite $0,4383 + 0,3606 i$ , ce qui peut être interprété comme la valeur pour laquelle $k$ est infini.

De telles séquences de tétration ont été étudiées depuis l'époque d'Euler mais sont très peu comprises en raison de leur comportement chaotique. Les recherches les plus publiées se sont historiquement concentrées sur la convergence de la fonction de tour de puissance. La recherche actuelle a grandement bénéficié du progrès de puissantes stations de calcul avec des supports logiciel en mathématiques symboliques et fractales. La plupart de ce qui est connu sur la tétration vient de la connaissance générale de la dynamique complexe et de la recherche spécifique sur les nappes exponentielles.

Extension aux nombres réels

L'extension de 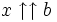$x \uparrow\uparrow b$ aux nombres réels $x > 0$ est relativement simple et donne, pour chaque nombre naturel $b$ , une fonction super-puissance 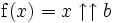$\operatorname{f}(x) = x \uparrow\uparrow b$ (le préfixe super est parfois remplacé par hyper : fonction hyper-puissance).

Comme indiqué précédemment, pour les entiers positifs $b$ , la fonction tends vers 1 pour $x$ tendant vers 0 si $b$ est pair, et vers 0 si $b$ est impair, alors que pour $b = 0$ et $b = - 1$ , la fonction est constante, avec pour valeur 1 et 0, respectivement.

À ce jour, il n'existe pas de solution communément acceptée pour le problème général d'extension de la tétration aux nombres réels et complexes, bien que cela soit un champ de recherche actif.

Considérons le problème de trouver une fonction super-exponentielle ou une fonction hyper-exponentielle 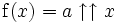$\operatorname{f}(x) = a \uparrow\uparrow x$ qui est une extension au réel $x > - 2$ de ce qui est défini précédemment, et qui satisfait (pour $a > 1$ ) :

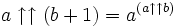$a \uparrow\uparrow(b+1) = a^{\left(a\uparrow \uparrow b\right)}$ .
une croissance monotone.
une condition de continuité.

Lorsque 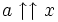$a \uparrow\uparrow x$ est définie comme un intervalle de longueur unitaire, la fonction dans son ensemble convient facilement pour tout $x > - 2$ .

Une solution simple est donnée par 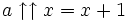$a \uparrow\uparrow x = x+1$ pour $- 1 < x < 0$ , par conséquent 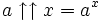$a \uparrow\uparrow x = a^x$ pour $0 < x < 1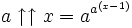$ , $\,\!a \uparrow\uparrow x=a^{a^{(x-1)}}$ pour $1 < x < 2$ , etc.

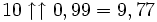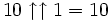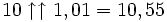Cependant, elle est différentiable par parties, à des valeurs entières de x, la dérivée est multipliée par $log n a$ : $10 \uparrow\uparrow 0,99 = 9,77$ , $10 \uparrow\uparrow 1 = 10$ , $10 \uparrow\uparrow 1,01 = 10,55$ .

D'autres fonctions, plus compliquées, peuvent être plus douces et/ou satisfont des propriétés additionnelles.

Une fonction super-exponentielle croît plus vite qu'une fonction double exponentielle; par exemple, si $a$ = 10:

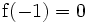
$\operatorname{f}(-1)=0$
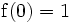
$\operatorname{f}(0)=1$
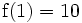
$\operatorname{f}(1)=10$
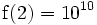
$\operatorname{f}(2)=10^{10}$
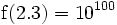$\operatorname{f}(2.3)=10^{100}$ (googol)
$\,\!\operatorname{f}(3)=10^{10^{10}}$
$\,\!\operatorname{f}(3.3)=10^{10^{100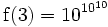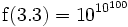}}$ (googolplex)
Cela devient 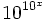$\,\!10^{10^x}$ pour $x = 2,376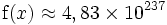$ : $\operatorname{f}(x) \approx 4,83 \times 10^{237}$

Lorsque l'on définit 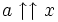$a \uparrow\uparrow x$ pour tout a, une autre condition requise peut être que 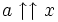$a \uparrow\uparrow x$ est croissante monotone avec a.

Ces fonctions inverses sont appelées super-racines ou hyper-racines, et super-logarithme ou hyper-logarithme $slog a$ définie pour tous les nombres réels, y compris les nombres négatifs.

La fonction $slog a$ satisfait à :

slog a a b = 1 + slog a b

slog a b = 1 + slog a log a b

slog a b > - 2

Exemples:

$slog 10 - 3 = - 1 + slog 10 0,001 = - 1 + - 0,999 = - 1,999$
$slog 10 3 = log 10 3 = 0,477$
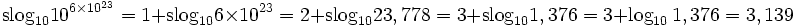
$\mathrm{slog}_{10} 10^{6\times 10^{23}} = 1 + \mathrm{slog}_{10} 6\times 10^{23} = 2 + \mathrm{slog}_{10} 23,778 = 3 + \mathrm{slog}_{10} 1,376 = 3 + \log_{10} 1,376 = 3,139$

Tours de puissance infiniment hautes

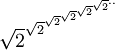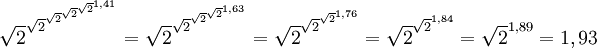$\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{..}}}}}}$ converge vers 2, et peut être en réalité définie comme étant égale à 2. La tendance vers 2 peut être perçue en évaluant une petite tour finie : $\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{1,41}}}}} = \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{1,63}}}} = \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{1,76}}} = \sqrt{2}^{\sqrt{2}^{1,84}} = \sqrt{2}^{1,89} = 1,93$ .

En général, la tour de puissance infinie 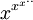$x^{x^{x^{..}}}$ converge pour $e - e < x < e 1 / e$ . Pour un réel quelconque $r$ avec $0 < r < e$ , puis $x = r 1 / r$ , alors la limite est $r$ . Il n'y a pas de convergence $x > e 1 / e$ (le maximum de $r 1 / r$ est $e 1 / e$ ).

Cela peut être étendu aux nombres complexes $z$ avec la définition :

$z^{z^{z^{.^{.^{.}}}}} = -\frac{\mathrm{W}(-\ln{z})}{\ln{z}}$

où $W(z)$ est la fonction W de Lambert.

Voir aussi

Fonction d'Ackermann

Références

Daniel Geisler, tetration.org
I.N. Galidakis, On extending hyper4 to nonintegers (non daté, 2006 ou plus tôt) (Une « revue » plus simple, plus facile à lire que la référence ci-dessous)
I.N. Galidakis, On Extending hyper4 and Knuth's Up-arrow Notation to the Reals (non daté, 2006 ou plus tôt).
Robert Munafo, Extension of the hyper4 function to reals (Discussion informelle de l'extension de la tétration aux nombres réels.)
Lode Vandevenne, Tetration of the Square Root of Two, (2004). (Essai d'extension de la tétration aux nombres réels.)
I.N. Galidakis, Mathématiques, (Liste définitive de références à la recherche sur la tétration. Informations nombreuses sur la fonction W de Lambert, les surfaces de Riemann et la continuation analytique.)
Galidakis, Ioannis and Weisstein, Eric W. Tour de puissance
Joseph MacDonell, Des points critiques sur la fonction hyperpuissance.
Dave L. Renfro, Web pages for infinitely iterated exponentials (Compilation des entrées à partir des questions sur la tétration sur sci.math.)
Andrew Robbins, Home of Tetration (Une extenstion infiniment différentiable sur la tétration des nombres réels.)
R. Knobel. "Exponentials Reiterated." American Mathematical Monthly 88, (1981), p. 235-252.
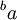Hans Maurer. "Über die Funktion $y=x^{[x^{[x(\cdots)]}]}$ für ganzzahliges Argument (Abundanzen)." Mittheilungen der Mathematische Gesellschaft in Hamburg 4, (1901), p. 33-50. (Référence à l'utilisation de $\ ^ba$ à partir de l'article de Knobel.)
Reuben Louis Goodstein. "Transfinite ordinals in recursive number theory." Journal of Symbolic Logic 12, (1947).

Liens externes

(en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Tetration ».

Portail des mathématiques

Ce document provient de « T%C3%A9tration ».

Catégories : Arithmétique | Grand nombre

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Tour de puissance de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Tour d'extension quadratique — En mathématiques et plus particulièrement en algèbre, dans le cadre de la théorie de Galois, une tour d extension quadratique est une suite de corps L0, L1, ...,Ln ayant les propriétés suivantes : si i est un entier entre 1 et n alors Li 1… … Wikipédia en Français
Tour eiffel — 48° 51′ 30″ N 2° 17′ 40″ E / 48.8583, 2.2945 … Wikipédia en Français
Tour Solaire — Schéma de principe Une tour solaire est une centrale à énergie renouvelable, construite de manière à canaliser l air chauffé par le soleil afin d actionner des turbines pour produire de l électricité. La première centrale a été construite par l… … Wikipédia en Français
Tour solaire — Schéma de principe Une tour solaire est une centrale à énergie renouvelable, construite de manière à canaliser l air chauffé par le soleil afin d actionner des turbines pour produire de l électricité. La première centrale a été construite par l… … Wikipédia en Français
Tour de transmission de radio varsovie — 52° 22′ 14″ N 19° 48′ 23″ E / 52.370555, 19.80639 … Wikipédia en Français
Puissance du Duelliste — est une extension de Yu Gi Oh! Jeu de cartes à jouer. « Fiche d identité » de l extension Monstre présent sur les boosters : Néos des Ténèbres, Héros Élémentaire (Ultra Rare) Nombre de cartes : 60 Année de sortie : 2006… … Wikipédia en Français
Tour métallique de Fourvière — Tour métallique de Fourvière. Présentation Période ou style Structure métallique Type Antenne relais Arch … Wikipédia en Français
puissance — [ pɥisɑ̃s ] n. f. • 1150; de puissant I ♦ (Sens faible) 1 ♦ Vx Puissance de... : moyen ou droit grâce auquel on peut (faire qqch.). ⇒ capacité. « La puissance de bien juger [...] est égale en tous les hommes » (Descartes). 2 ♦ Mod. Philos.… … Encyclopédie Universelle
Tour 2009 de Mylène Farmer — Tour 2009 Tournée de Mylène Farmer Début de la tournée 2 mai 2009 Fin de la tournée 19 septembre 2009 Durée 4 mois Producteur(s) de la tournée Thierry Suc Titres de la … Wikipédia en Français
Tour de Blosenberg — Localisation Coordonnées … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Tour de puissance

Tétration

Sommaire

Notation

Exemples

Extension aux valeurs faibles du second opérand

Tétration complexe

Extension aux nombres réels

Tours de puissance infiniment hautes

Voir aussi

Références

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Tour de puissance

Tétration

Sommaire

Notation

Exemples

Extension aux valeurs faibles du second opérand

Tétration complexe

Extension aux nombres réels

Tours de puissance infiniment hautes

Voir aussi

Références

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link