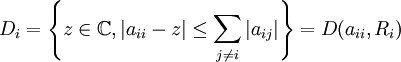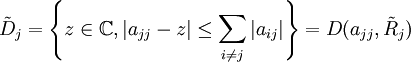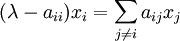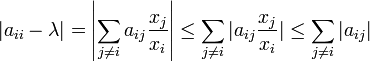Théorème de gershgorin

Théorème de gershgorin

Théorème de Gerschgorin

En analyse numérique, le théorème de Gerschgorin est un résultat permettant de borner a priori les valeurs propres d'une matrice carrée. Il a été publié en 1931 par le mathématicien biélorusse Semion Aronovitch Gershgorin. Son nom peut être transcrit de diverses manières : Gershgorin, Gerschgorin ou Geršgorin.

Sommaire

Le théorème

Énoncé

Soit A une matrice complexe de taille n×n, de terme général (aij). Pour chaque indice de ligne i entre 1, et n on introduit le disque de Gerschgorin correspondant

D_i=\left\{z\in \mathbb{C}, |a_{ii}-z|\leq \sum_{j\neq i}|a_{ij}| \right\}=D(a_{ii},R_i)

qui constitue effectivement un disque dans le plan complexe, de rayon Ri.

Théorème: toute valeur propre de A appartient à l'un au moins des disques de Gerschgorin.

En appliquant le théorème à la matrice transposée de A, une nouvelle information est donnée sur la localisation des valeurs propres : elles se trouvent dans la réunion des disques de Gerschgorin associés aux colonnes

\tilde{D}_j=\left\{z\in \mathbb{C}, |a_{jj}-z|\leq \sum_{i\neq j}|a_{ij}| \right\}=D(a_{jj},\tilde{R}_j)

Démonstration

Soient λ une valeur propre de A et x = (x1, ..., xn) un vecteur propre associé. Pour i compris entre 1 et n, on a

(\lambda - a_{ii})x_i = \sum_{j\neq i} a_{ij}x_j

Choisissons un indice i pour lequel le module de xi est maximal. Puisque x est un vecteur propre, |xi| est non nul et il est possible de former le quotient

|a_{ii} - \lambda| = \left|\sum_{j\neq i} a_{ij}\frac{x_j}{x_i}\right| \leq \sum_{j\neq i} |a_{ij}\frac{x_j}{x_i}| \leq \sum_{j\neq i} |a_{ij}|

Voir aussi

Ovale de Cassini

Références

  • Patrick Lascaux, Raymond Théodor, Analyse numérique matricielle appliquée à l'art de l'ingénieur, tome 1 : Méthodes directes [détail des éditions]
  • (de) Gerschgorin, S. "Über die Abgrenzung der Eigenwerte einer Matrix." Izv. Akad. Nauk. USSR Otd. Fiz.-Mat. Nauk 7, 749-754, 1931
  • (en) Varga, R. S. Geršgorin and His Circles. Berlin: Springer-Verlag, 2004. ISBN 3-540-21100-4. Errata.

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Gerschgorin ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de gershgorin de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Theoreme de Gershgorin — Théorème de Gerschgorin En analyse numérique, le théorème de Gerschgorin est un résultat permettant de borner a priori les valeurs propres d une matrice carrée. Il a été publié en 1931 par le mathématicien biélorusse Semion Aronovitch Gershgorin …   Wikipédia en Français

  • Théorème de Gershgorin — Théorème de Gerschgorin En analyse numérique, le théorème de Gerschgorin est un résultat permettant de borner a priori les valeurs propres d une matrice carrée. Il a été publié en 1931 par le mathématicien biélorusse Semion Aronovitch Gershgorin …   Wikipédia en Français

  • Théorème de Gerschgorin — En analyse numérique, le théorème de Gerschgorin est un résultat permettant de borner a priori les valeurs propres d une matrice carrée. Il a été publié en 1931 par le mathématicien biélorusse Semyon Aranovich Gershgorin (en). Son nom peut… …   Wikipédia en Français

  • Théorie des équations (mathématiques) — Pour les articles homonymes, voir Théorie des équations. La théorie des équations est la partie des mathématiques qui traite des problèmes posés par les équations polynomiales de tous les degrés. Se trouvent ainsi rassemblés les problèmes de… …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Matrice diagonale — En algèbre linéaire, une matrice diagonale est une matrice carrée dont les coefficients en dehors de la diagonale principale sont nuls. Les coefficients de la diagonale peuvent être ou ne pas être nuls. Ainsi, la matrice D = (di,j) est diagonale… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”