Theorie Elo

Classement Elo

Pour les articles homonymes, voir Elo.

Le classement Elo est un système d'évaluation du niveau de capacités relatif d'un joueur d'échecs ou de jeu de go, ou d'autres jeux à deux joueurs. Plus généralement, il peut servir à comparer deux joueurs d'une partie, et est utilisé par de nombreux jeux en ligne.

Elo se trouve parfois écrit par erreur en haut de casse ELO. Or, il ne s'agit pas d'un acronyme. Il doit son nom à Arpad Elo (1903-1992), un professeur de physique et excellent joueur d'échecs américain d'origine hongroise qui l'a mis au point.

Sommaire

1 Théorie Elo
2 Mode de calcul
- 2.1 Calcul du classement FIDE
3 Statistiques
4 Niveau de jeu en fonction du nombre de points
- 4.1 Les numéros un mondiaux
5 Classement
6 Références
7 Voir aussi

Théorie Elo

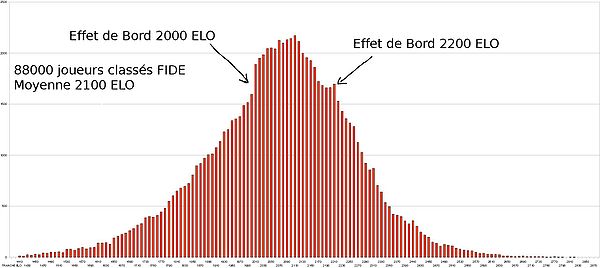
La formule d'Elo repose sur la résolution d’une équation différentielle avec une hypothèse qui se vérifie relativement bien. Ce qui explique les petites différences que l’on peut constater entre le système Elo et la loi normale.

Prenons 3 joueurs a, b, c. Les notations $P (a / b)$ , $P (a / c)$ , $P (b / c)$ expriment respectivement la probabilité que a gagne contre b ; la probabilité que a gagne contre c et pour finir la probabilité que b gagne contre c.

On peut écrire : 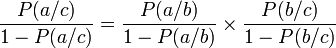$\frac{P(a/c)}{1-P(a/c)}=\frac{P(a/b)}{1-P(a/b)}\times\frac{P(b/c)}{1-P(b/c)}$ {1}
Explication : si on note Fac le membre de gauche, ça représente la force de a contre c. La formule devient :

Fac = Fab.Fbc, ce qui est admissible : les forces se multiplient.

Remarque : cette formule est très fausse avec quelques parties et devient de plus en plus vraie quand le nombre de parties disputées grandit.

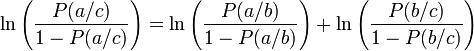$\ln\left(\frac{P(a/c)}{1-P(a/c)}\right)=\ln\left(\frac{P(a/b)}{1-P(a/b)}\right)+\ln\left(\frac{P(b/c)}{1-P(b/c)}\right)$ {2}
Posons :

{3} 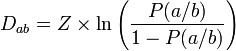$D_{ab}=Z\times\ln\left(\frac{P(a/b)}{1-P(a/b)}\right)$ ; de même pour

D a c

D b c

Nous obtenons : $D a c = D a b + D b c$ {4}
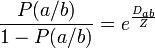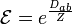On peut prendre la fonction inverse de [3] : $\frac{P(a/b)}{1-P(a/b)}=e^{\frac{D_{ab}}{Z}}$ ; posons : $\mathcal{E}= e^{\frac{D_{ab}}{Z}}$ .
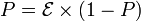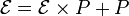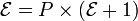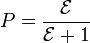En résolvant, on trouve : $P=\mathcal{E}\times(1-P)$ ; $\mathcal{E}=\mathcal{E}\times P+P$ ; $\mathcal{E}=P \times (\mathcal{E}+1)$ ; $P=\frac{\mathcal{E}}{\mathcal{E}+1}$ ;

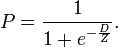
{6} : $P=\frac{1}{1+e^{- \frac{D}{Z}}}.$

En différenciant, on trouve :

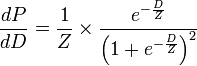$\frac{dP}{dD}=\frac{1}{Z}\times\frac{e^{- \frac{D}{Z}}}{\left(1+e^{- \frac{D}{Z}}\right)^2}$ {7}, qui est la distribution de Verhulst.

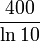On prendra D égal à la différence de classement et Z égal à $\frac{400}{\ln10}$ .

Mode de calcul

Les fédérations nationales utilisent souvent un système légèrement différent de celui de la Fédération internationale des échecs (FIDE).

Il existe souvent deux classements distincts : l'un au niveau international, géré par la FIDE, et dit « Classement FIDE » ou « Classement international », et un au niveau national, géré en France par la FFE, par la FQE au Québec, par la FCE au Canada et par la FSE en Suisse, dit « Elo national ». Un joueur peut disposer à la fois d'un classement international et d'un ou plusieurs classements nationaux qui évoluent indépendamment.

Jusqu'en 1993, le seuil minimal du classement FIDE était fixé à 2200^[1], soit le niveau d'un candidat maître, les amateurs ne disposaient que du classement national. Il a été abaissé progressivement jusqu'à atteindre 1200 depuis le 1^er juillet 2009, soit le niveau d'un joueur de club moyen, et l'intention de la FIDE est de le baisser jusqu'à 1000^[2], qui est le niveau d'un débutant.

Depuis le 1^er juillet 2009, la différence maximale entre deux classements pour le calcul des points gagnés / perdus après chaque partie a été ramenée à 400 points au lieu de 350 précédemment.

Calcul du classement FIDE

Nombre de classés FIDE par tranche Elo (données 2008)

Premier classement

Dans un système suisse où le joueur rencontre au moins trois joueurs classés FIDE :

on détermine le classement moyen des adversaires, R_c.
on calcule le pourcentage de gain contre ces adversaires, p (c'est-à-dire la somme des points obtenus divisée par le nombre de parties)
on détermine d(p) en fonction de la table 10.1^[3]
si p < 0,5, alors R_u=R_c + d(p)
si p = 0,5, alors R_u=R_c
si p > 0,5, alors R_u=R_c + 12,5 points par demi-point obtenu au-dessus de 50%

Dès qu'il existe 9 parties jouées, le premier classement publié sera égal à la moyenne pondérée des R_u de chaque tournoi, arrondie à l'entier le plus proche, si toutefois celle-ci dépasse 1400.

Par exemple, un joueur qui joue trois tournois :

dans le premier, il réalise un R_u=2280 sur 5 parties
dans le second, R_u=2400 sur 10 parties
dans le troisième, R_u=2000 sur 5 parties

Son premier classement sera :

Rn = ( 2280 x 5 + 2400 x 10 + 2000 x 5 ) / 20 = 2270.

Classement habituel

Pour chaque partie jouée contre un joueur classé FIDE :

on détermine la différence d de classement entre le joueur adverse et le sien (ramenée à 400 si elle dépasse 400 depuis le 1^er juillet 2009 - au lieu de 350 avant cette date)
on détermine p(d) à l'aide de la table 10.2^[3]
on détermine un coefficient K qui vaudra :
- K=25 jusqu'à la 30^e partie du joueur, sinon
- K=15 en-dessous de 2400, sinon
- K=10 au-dessus de 2400, et reste à cette valeur ensuite.
soit W le résultat contre l'adversaire (W=1, ½ ou 0), le nouveau classement sera :
R_n = R_o + K x (W - p(d))

Par exemple, si un joueur classé 2600 gagne contre un joueur classé 2700, son nouveau classement sera : 2600 + 10 x ( 1 - 0,36 ) = 2606,4. Pour la publication, on arrondira à l'entier le plus proche.

Le classement FIDE est mis à jour quatre fois par an, et publié le 1^er janvier, 1^er avril, 1^er juillet et 1^er octobre. Si un joueur a moins de quatre parties classées sur une période d'un an, il est considéré comme inactif. Si le classement passe en-dessous de seuil FIDE (1400), il sera retiré de la liste et à nouveau considéré comme un non-classé.

Performance Elo

On utilise la notion de performance Elo pour caractériser la force d'un joueur dans un tournoi, en fonction de la moyenne des classements Elo des adversaires (R_c) et du résultat contre ceux-ci (p), elle est aussi parfois employée comme système de départage d'un tournoi au système suisse :

R_p=R_c + d(p)

Statistiques

En 2008 :

Joueur classé 1^er le plus de fois : Garry Kasparov (23 fois).
Plus jeune joueur classé parmi les 100 premiers : Fabiano Caruana
Plus jeune joueur parmi les 10 premiers: Magnus Carlsen 2786 4ème
Plus vieux joueur classé parmi les 100 premiers : Viktor Kortchnoï (76 ans - N°85).

Au 1^er juillet 2008, seuls 4 joueurs avaient dépassé les 2 800 points : Garry Kasparov (2 851 points), Veselin Topalov (2 813 points), Vladimir Kramnik (2 811 points) et Viswanathan Anand (2 803).

Niveau de jeu en fonction du nombre de points

Ces éléments sont donnés à titre indicatif. Les titres sont attribués par la FIDE en fonction de performances réalisées lors de compétitions et si le prétendant a obtenu un classement Elo requis. Ils sont ensuite acquis à vie et le classement d'un maître peut ensuite être inférieur à ce minimum.

> 1000 : Débutant (enfant)
> 1200 : Débutant
> 1400 : Joueur amateur
> 1600 : Bon joueur
> 1800 : Très bon joueur
> 2000 : Niveau national
> 2200 : candidat maître
> 2300 : Maître FIDE
> 2400 : Maître international (~ 2565 joueurs)
> 2500 : Grand maître international (~ 900 joueurs)
> 2600 : Les 200 meilleurs joueurs mondiaux
> 2700 : Les 30 meilleurs joueurs mondiaux
> 2800 : Seuls Garry Kasparov, Vladimir Kramnik, Veselin Topalov et Viswanathan Anand ont dépassé les 2800 points

Les numéros un mondiaux

Depuis l'adoption du classement par la FIDE en 1970, seuls six joueurs ont été classés à la première place. Garry Kasparov est le joueur ayant obtenu le plus haut classement et celui étant resté numéro un le plus longtemps^[4].

Période	Nom	Elo max
1970 — janvier 1976	Bobby Fischer	2785
janvier 1976 — janvier 1984	Anatoli Karpov	2725
janvier 1984 — janvier 1996	Garry Kasparov	2815
janvier — avril 1996	Garry Kasparov et Vladimir Kramnik	2775
avril 1996 — avril 2006	Garry Kasparov	2851
avril 2006 — avril 2007	Veselin Topalov	2813
avril 2007 — janvier 2008	Viswanathan Anand	2801
janvier — avril 2008	Viswanathan Anand et Vladimir Kramnik	2799
avril — octobre 2008	Viswanathan Anand	2803
octobre 2008 — juillet 2009	Veselin Topalov	2813

N.B. Le classement Elo maximum indiqué est celui de la période considérée (ce qui ne correspond pas toujours au meilleur classement Elo du joueur).

Classement

**Liste des 10 premiers mondiaux au 1^er septembre 2009**
Rang	Ancien rang	Nom	Nation	Elo (variation)	Parties jouées	Né en
1	1	Veselin Topalov	Bulgarie	2813 (0)	0	1975
2	2	Viswanathan Anand	Inde	2788 (0)	0	1969
3	4	Levon Aronian	Arménie	2773 (+5)	13	1982
4	3	Magnus Carlsen	Norvège	2772 (0)	10	1990
5	6	Vladimir Kramnik	Russie	2772 (+13)	10	1975
6	7	Péter Lékó	Hongrie	2762 (+3)	23	1979
7	8	Teimour Radjabov	Azerbaïdjan	2757 (+1)	10	1987
8	30	Vassili Ivantchouk	Ukraine	2756 (+53)	42	1969
9	9	Boris Gelfand	Israël	2756 (+1)	33	1968
10	10	Aleksandr Morozevitch	Russie	2750 (-1)	18	1977

Moyenne Elo 2769,9 (+2,1)

Cette liste est établie tous les 2 mois et les variations concernent la différence avec la liste du 1^er juillet 2009.

Source : Top10 Hommes sur fide.com

Références

↑ The Scotsman 2002
↑ Congrès 2000
↑ ^{a et b} Table d(p)
↑ [1] pour la période 1970 — 1997, et le site de la FIDE pour la période 2000 -2009

Voir aussi

Portail des échecs

Ce document provient de « Classement Elo ».

Catégorie : Compétition d'échecs

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theorie Elo de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Théorie Elo — Classement Elo Pour les articles homonymes, voir Elo. Échecs Le classement Elo est un système d évaluation du niveau de capacités relatif d un … Wikipédia en Français
ELO-Zahl — Schach Go Das Elo System ist ein objektives Wertungssystem, das es erlaubt, die Spielstärke von Go und Schachspielern durch eine Wertungszahl (kurz: Elo Zahl) zu bes … Deutsch Wikipedia
Elo-System — Schach Go Das Elo System ist ein objektives Wertungssystem, das es erlaubt, die Spielstärke von Go und Schachspielern durch eine Wertungszahl (kurz: Elo Zahl) zu bes … Deutsch Wikipedia
Elo-Zahl — Schach Go Die Elo Zahl ist eine Wertungszahl, die die Spielstärke von … Deutsch Wikipedia
Élő — Arpad Elo Arpad Emrick Elo (né Élő Árpád Imre 25 août 1903 à Egyházaskesző, Hongrie 5 novembre 1992 à Brookfield, Wisconsin, États Unis) est un scientifique, mathématicien et joueur d échecs d origine hongroise. Il est surtout … Wikipédia en Français
Classement Elo — Pour les articles homonymes, voir Elo. Pièces d’un jeu d’échecs. Le classement Elo est un système d’évaluation du niveau de capacités relatif d’un joueur d’échecs … Wikipédia en Français
Classement elo — Pour les articles homonymes, voir Elo. Échecs Le classement Elo est un système d évaluation du niveau de capacités relatif d un … Wikipédia en Français
Classement mondial elo — Classement Elo Pour les articles homonymes, voir Elo. Échecs Le classement Elo est un système d évaluation du niveau de capacités relatif d un … Wikipédia en Français
World Football Elo Ratings — (dt. etwa Weltfußball Elo Rangskala ) ist ein Ranglistensystem für A Nationalmannschaften im Fußball. Es basiert auf der Methode der Elo Zahl, ist aber modifiziert, um verschiedene fußballspezifische Variablen mit einzubeziehen . Es ist eine… … Deutsch Wikipedia
Arpad Emrick Elo — Arpad Elo Arpad Emrick Elo (né Élő Árpád Imre 25 août 1903 à Egyházaskesző, Hongrie 5 novembre 1992 à Brookfield, Wisconsin, États Unis) est un scientifique, mathématicien et joueur d échecs d origine hongroise. Il est surtout … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theorie Elo

Classement Elo

Sommaire

Théorie Elo