Theoreme de preparation de Weierstrass

Theoreme de preparation de Weierstrass

Théorème de préparation de Weierstrass

En mathématiques, le théorème de préparation de Weierstrass est un outil utilisé dans la théorie des fonctions analytiques de plusieurs variables.

Il affirme qu'au voisinage d'un point P, une telle fonction est le produit d'une fonction non nulle en P, et d'un polynôme unitaire 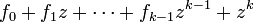f_0 + f_1 z + \cdots + f_{k-1} z^{k-1} + z^k en l'une des variables z, où les fi sont des fonctions analytiques des autres variables et vérifient fi(P) = 0.

Ce théorème possède de nombreux analogues ou variantes, encore désignés sous le nom de théorème de préparation de Weierstrass. Par exemple, on dispose du résultat suivant sur les séries formelles à coefficients dans l'anneau 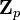\mathbf{Z}_p des entiers p-adiques, où p est un nombre premier.

Soit 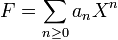F = \sum_{n \geq 0} a_n X^n une série formelle à coefficients dans 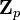\mathbf{Z}_p . On suppose que F n'est pas divisible par p, c'est-à-dire qu'au moins l'un des coefficients de F n'est pas divisible par p. On note k l'entier minimal tel que ak n'est pas divisible par p. Alors il existe un polynôme G de \mathbf{Z}_p[X] et une série formelle H de \mathbf{Z}_p[[X]] tels que

(1) F = GH

(2) G est unitaire de degré k et H est inversible dans \mathbf{Z}_p[[X]] .

De plus, G et H sont déterminés de manière unique.

Remarque. Dans le cas particulier où F est un polynôme de degré N et 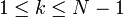1 \leq k \leq N-1 , on peut montrer que H est un polynôme de degré N − k, ce qui fournit une factorisation non triviale de F. Ce résultat s'apparente au lemme de Hensel : on passe d'une factorisation dans \mathbf{Z}/p\mathbf{Z}[X] à une factorisation dans \mathbf{Z}_p[X] .

L'analogie avec le théorème concernant les fonctions analytiques vient du fait que les éléments de 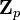\mathbf{Z}_p peuvent être considérés comme des séries entières en la variable p, via le développement de Hensel.



  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de pr%C3%A9paration de Weierstrass ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de preparation de Weierstrass de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Théorème de préparation de Weierstrass — Pour les articles homonymes, voir Théorème de Weierstrass. En mathématiques, le théorème de préparation de Weierstrass désignait dans un premier temps un outil utilisé dans la théorie des fonctions analytiques de plusieurs variables complexes. L… …   Wikipédia en Français

  • Théorème de préparation de weierstrass — …   Wikipédia en Français

  • Théorème de Weierstrass — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs théorèmes sont attribués à Karl Weierstrass ou le mentionnent dans leur nom. Théorème de Bolzano Weierstrass Théorème de factorisation de… …   Wikipédia en Français

  • Karl Weierstrass — Karl Theodor Wilhelm Weierstrass Naissance 31 octobre 1815 Ostenfelde en Westphalie ( …   Wikipédia en Français

  • Malgrange preparation theorem — In mathematics, the Malgrange preparation theorem is an analogue of the Weierstrass preparation theorem for smooth functions. It was conjectured by René Thom and proved by B. Malgrange (1962–1963, 1964, 1967). Contents 1 Statement of… …   Wikipedia

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”