Theodolite

Un théodolite est un instrument de géodésie complété d’un instrument d’optique, mesurant des angles dans les deux plans horizontal et vertical afin de déterminer une direction. Il est utilisé pour réaliser les mesures d’une triangulation : mesure des angles d’un triangle.

C'est un instrument essentiel en topographie et en ingénierie.

Sommaire 1 Étymologie 2 Description 3 Emploi du théodolite en topographie 4 Liens externes

Étymologie

Un théodolite a d’abord désigné un instrument d’arpentage (1704). Le mot pourrait avoir été emprunté au latin scientifique theodolitus. L’instrument aurait été inventé en 1571 par un anglais, Thomas Digges qui l’aurait nommé ainsi. En anglais, l’emploi du terme theodolite est attesté en 1607.

L’étymologie est incertaine. Le theos signifiant « dieu » n’aide pas plus que le dêlos signifiant « visible ».

Description

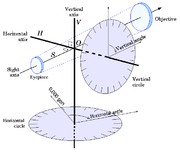
Un théodolite est une lunette montée sur les deux axes vertical et horizontal. Chacun des axes est équipé d’un cercle gradué permettant les lectures des angles.

Le théodolite se pose sur un support et doit se caler sur le plan horizontal ; il est souvent placé sur un trépied, et à la verticale exacte d’un point connu en coordonnées, à l’aide d’un fil à plomb et d’un niveau à bulle sphérique, et sa base doit être parfaitement horizontale (utilisation d’une nivelle torique, ainsi que d’une nivelle sphérique). L’ensemble de cette phase d’utilisation se nomme la « mise en station ».

Le théodolite fait partie de la famille des instruments de mesure d’angles.

En astronomie, le théodolite sert à déterminer l’azimut par rapport au pôle céleste, ou la déclinaison où la hauteur apparente d’un corps céleste par rapport à l’horizon.

En géodésie, il sert à déterminer les angles formés par 3 sommets de montagne par exemple.

En topographie, il est utilisé dans les mesures d’un levé du territoire (levé topographique).

En archéologie, lors de fouilles, il est utilisé comme instrument de mesure de points spécifiques du relief, utilisés ensuite dans la reconstitution du site en trois dimensions.

Les instruments servant seulement aux mesures des angles horizontaux sont des goniomètres, ceux servant seulement à la mesure des angles verticaux sont des éclimètres et ceux permettant à la fois la mesure des angles horizontaux et des angles verticaux sont des théodolites.

Le théodolite peut être associé à différents instruments permettant par exemple la mesure des distances, on parle alors de tachéomètre, ou la saisie automatique des mesures, on parle alors de station totale.

Emploi du théodolite en topographie

Le théodolite est en gros un rapporteur perfectionné, qui permet de relever l’angle entre deux points. On s’en sert pour des travaux de topographie. En fait, ce qu’on mesure n’est pas directement l’angle entre deux repères visibles (signaux sur une montagne, clocher…), mais entre la verticale de ces signaux, c’est-à-dire qu’on fait abstraction de la hauteur à laquelle les repères sont visibles, pour n’en retenir que le gisement (les verticaux des signaux visibles). On cale donc le théodolite à l’horizontale, et les angles ne sont mesurés que dans le plan horizontal, avec une petite lunette de visée qui peut pivoter verticalement, pour viser en hauteur.

Pour améliorer la précision des relevés dans un triangle ABC, on mesure en fait les trois angles en A, B, et C. Ces mesures sont redondantes, la somme des angles devant être 180°. En fait, on trouve toujours une petite différence dans la mesure : on considère que cette différence vient d’erreurs aléatoires, et on corrige les relevés en soustrayant 1/3 de la différence à chacune des valeurs. Pour les relevés à petite distance, la géométrie est pratiquement plane, mais à grande distance et avec un relevé de précision que permet le théodolite, la courbure de la Terre se fait sentir : la somme des angles d’un triangle ne fait plus 180°, mais dépend aussi de la surface du triangle inscrit. Dans les travaux de triangulation à longue distance, par exemple pour mesurer le méridien terrestre, on est donc obligé de tenir compte de cette correction (calcul en trigonométrie sphérique) avant de corriger les relevés, qui sinon seraient systématiquement faussés.

Les conditions de bonne visibilité et le relief permettent en France de travailler sur des visées de 40 à 50 kilomètres en plaine, un peu plus sur des points élevés isolés. Les angles sont lus, avec les meilleurs théodolites, avec une précision de l’ordre du décimilligrade ; on fait les observations et les calculs avec un chiffre de plus pour ne pas dégrader la précision avec des erreurs d’arrondi. L’excès sphérique d’un polygone est environ de 1,6 dmgr pour 100 km² de surface. Pour un triangle de 40 km de côtés, il peut atteindre 14 dmgr, ce qui est loin d’être négligeable (un décimilligrade est l’angle sous lequel, à 40 km, on verrait un objet d’environ 6 centimètres - d'où une erreur pouvant atteindre près de 84 cm).

Liens externes

• (fr) Astrosurf : Le Théodolite

• Portail de l’information géographique
• Portail de l’archéologie
• Portail du bâtiment et des travaux publics