Temps d'arret

Temps d'arret

Temps d'arrêt

Sommaire

Définitions

Définition — Une variable aléatoire 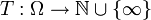T : \Omega \rightarrow \mathbb N \cup \{ \infty \} est un temps d'arrêt par rapport à une filtration 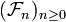(\mathcal{F}_n)_{n\ge 0} si,

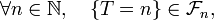
\forall n \in \mathbb N,\quad\{T=n\} \in \mathcal{F}_n,

ou bien, équivalemment, si,

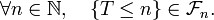
\forall n \in \mathbb N,\quad\{T\le n\} \in \mathcal{F}_n.

Interprétation

Imaginons que 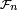\scriptstyle\ \mathcal{F}_n\ désigne ici la tribu engendrée par la suite 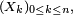\scriptstyle\ (X_k)_{0\le k\le n},\ et que les variables aléatoires 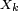\scriptstyle\ X_k\ représentent les résultats d'un joueur lors des parties successives d'un jeu. Dans le cas de variables aléatoires à valeurs dans un espace d'états 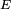\scriptstyle\ E\ fini ou dénombrable, une partie 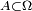\scriptstyle\ A\subset \Omega\ appartient à 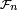\scriptstyle\ \mathcal{F}_n\ si et seulement si il existe 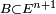\scriptstyle\ B\subset E^{n+1}\ tel que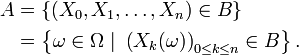

\begin{align} A &= \left\{(X_0,X_1,\dots,X_n)\in B\right\} \\ &= \left\{\omega\in\Omega\ |\ \left(X_k(\omega)\right)_{0\le k\le n}\in B\right\}. \end{align}

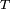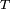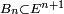Supposons que \scriptstyle\ T\ représente le numéro de la partie après laquelle le joueur décide d'arrêter de jouer : \scriptstyle\ T\ est donc un temps d'arrêt si et seulement si la décision d'arrêter est prise en fonction des résultats des parties déjà jouées au moment de l'arrêt, i.e. si pour tout \scriptstyle\ n\ il existe un sous ensemble \scriptstyle\ B_n\subset E^{n+1}\ tel que  :

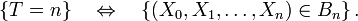
\{T=n\}\quad \Leftrightarrow\quad\left\{(X_0,X_1,\dots,X_n)\in B_n\right\}.

L'instant où le joueur s'arrête est donc un temps d'arrêt si la décision d'arrêt ne tient pas compte des résultats des parties futures, donc sous l'hypothèse que don de double-vue et tricherie sont exclus.

Notations

  • Soient 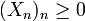(X_n)_n\ge 0\ une suite de variables aléatoires (un processus stochastique) et T un temps d'arrêt par rapport à une filtration 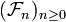(\mathcal{F}_n)_{n\ge 0}. Le processus observé au temps T (ou arrêté au temps T) est noté 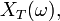\ X_T(\omega),\ et est défini par
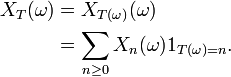
\begin{align}X_T(\omega)&=X_{T(\omega)}(\omega)\\ &=\sum_{n\ge 0}X_n(\omega)1_{T(\omega)=n}. \end{align}
Sur l'ensemble 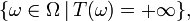\{\omega\in\Omega\,|\,T(\omega)=+\infty\},\ la définition de 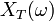\ X_T(\omega)\ est problèmatique : l'ambiguité est de facto levée en posant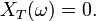 \ X_T(\omega)=0.\
  • Soit 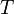T \, un temps d'arrêt et soi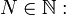 N \in \mathbb N :
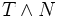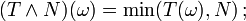
    • T \wedge N est la variable aléatoire définie par (T \wedge N)(\omega)=\min(T(\omega),N)\,;
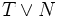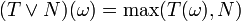    • T \vee N est la variable aléatoire définie par (T \vee N)(\omega)=\max(T(\omega),N) \,.

Propriétés

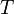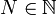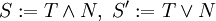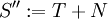Propriété — Soit T\, un temps d'arrêt, soit N\in \mathbb N. Alors S:= T \wedge N,\ S^{\prime}:=T \vee N\ et \ S^{\prime\prime}:=T+N\ sont des temps d'arrêt.

Démonstration

On ne démontrera que le premier point, les deux autres étant semblables :

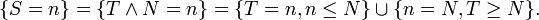
\{ S =n \} = \{ T\wedge N =n \} = \{ T=n , n \le N \} \cup \{ n=N , T \ge N\}.

Or

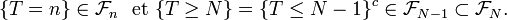
\{ T=n \} \in \mathcal{F}_n \ \text{ et } \{ T \ge N\} = \{ T \le N-1 \}^c \in \mathcal{F}_{N-1}\subset\mathcal{F}_{N}.

Propriété — De même, si 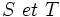S\ et \ T sont des temps d'arrêts, alors 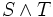S\wedge T en est un.

Définition et propriété — Soit 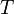T\, un temps d'arrêt et 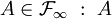A \in \mathcal{F}_\infty\ :\ A\, est appelé évènement antérieur à 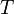T\, si:

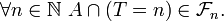
\forall n \in \mathbb N \ A \cap (T=n) \in \mathcal{F}_n.

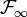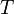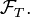L'ensemble de ces évènements forme une sous-tribu de \mathcal{F}_\infty appelée tribu antérieure à T\, et notée \mathcal{F}_T.

Démonstration
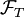  • \mathcal{F}_T contient \Omega \,
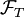  • \mathcal{F}_T est stable par réunion dénombrable
  • Soit 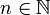n\in \mathbb N. On a 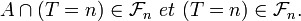A \cap (T=n) \in \mathcal{F}_n\ et \ (T=n) \in \mathcal{F}_n.\ D'où
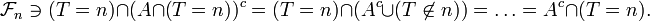
\mathcal{F}_n \ni (T=n) \cap (A \cap (T=n))^c = (T=n) \cap (A^c \cup (T\not\in n)) =\ldots =A^c \cap (T=n).

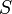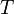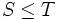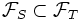Proposition — Soient S\, et T\, deux temps d'arrêts tels que S\le T p.s.. On a alors \mathcal{F}_S \subset \mathcal{F}_T.

Démonstration

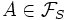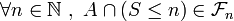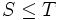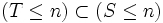Soit A \in \mathcal{F}_S, c’est-à-dire \forall n\in \mathbb N\ ,\ A\cap (S\le n) \in \mathcal{F}_n. Comme de plus S\le T\, p.s., (T\le n)\subset (S\le n). Par suite,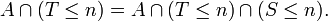

A\cap (T\le n) = A\cap (T\le n)\cap (S\le n).

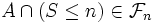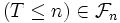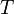Or A\cap (S\le n) \in \mathcal{F}_n et (T\le n)\in \mathcal{F}_n car T\, est un temps d'arrêt. Donc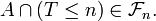

A\cap (T\le n) \in \mathcal{F}_n.

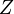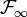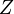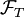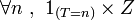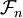Lemme — Soit Z\, une variable aléatoire \mathcal{F}_\infty-mesurable. Z\, est \mathcal{F}_T-mesurable ssi \forall n\ ,\ 1_{(T=n)}\times Z est \mathcal{F}_n-mesurable.

Démonstration

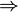\Rightarrow :

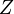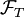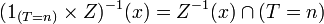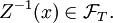
Z\, est \mathcal{F}_T-mesurable. (1_{(T=n)}\times Z)^{-1}(x)=Z^{-1}(x) \cap (T=n) avec Z^{-1}(x)\in \mathcal{F}_T.

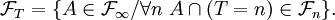
Or \mathcal{F}_T = \{ A \in \mathcal{F}_\infty / \forall n \ A\cap (T=n)\in \mathcal{F}_n \}.

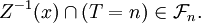
Donc Z^{-1}(x) \cap (T=n) \in \mathcal{F}_n.

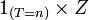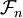Finalement 1_{(T=n)}\times Z\, est \mathcal{F}_n-mesurable.

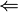\Leftarrow :

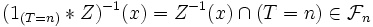
(1_{(T=n)}*Z)^{-1}(x) = Z^{-1}(x) \cap (T=n) \in \mathcal{F}_n

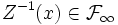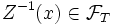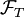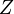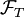avec de plus Z^{-1}(x) \in \mathcal{F}_\infty. D'où Z^{-1}(x)\in \mathcal{F}_T (d'après la définition de \mathcal{F}_T). Donc Z\, est \mathcal{F}_T-mesurable.

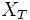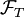Proposition — X_T\, est \mathcal{F}_T-mesurable.

Démonstration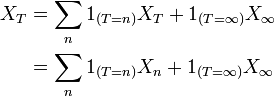
\begin{align} X_T&=\sum_n 1_{(T=n)}X_T + 1_{(T=\infty)}X_\infty \\ &=\sum_n 1_{(T=n)}X_n + 1_{(T=\infty)}X_\infty\end{align}

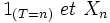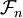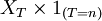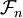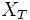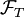avec 1_{(T=n)}\ et\ X_n qui sont \mathcal{F}_n-mesurable, d'où X_T\times 1_{(T=n)}\, est \mathcal{F}_n-mesurable. D'après le lemme précédent, X_T\, est \mathcal{F}_T-mesurable.

Exemples et contrexemples

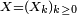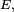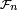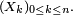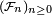Considérons une suite \scriptstyle\ X=(X_k)_{k\ge 0}\ de variable aléatoires, à valeurs dans un ensemble \scriptstyle\ E,\ et notons \scriptstyle\ \mathcal{F}_n\ la tribu engendrée par la suite \scriptstyle\ (X_k)_{0\le k\le n}.\ Les variables aléatoires ci-dessous sont des temps d'arrêt pour la filtration \scriptstyle\ (\mathcal{F}_n)_{n\ge 0} :

  • Soit 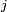\scriptstyle\ j\ un élément de 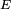\scriptstyle\ E\  ; on appelle instant de premier retour en 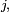\scriptstyle\ j,\ et on note 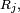\scriptstyle\ R_j,\ la variable aléatoire définie ci-dessous :
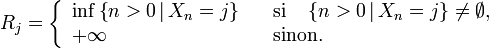
R_j = \left\{ \begin{array}{lll} \inf\left\{n > 0\,\vert\,X_n = j\right\}& &\textrm{si }\quad\left\{n > 0\,\vert\,X_n = j\right\} \neq\emptyset,\\ +\infty& &\textrm{sinon.} \end{array} \right.
  • De même pour 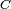\scriptstyle\ C\ une partie de 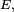\scriptstyle\ E,\ on appelle instant de première entrée dans 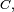\scriptstyle\ C,\ et on note 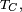\scriptstyle\ T_C,\ la variable aléatoire ci-dessous définie :
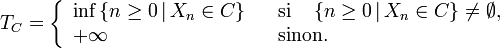
T_C = \left\{ \begin{array}{lll} \inf\left\{n \ge 0\,\vert\,X_n \in C\right\}& &\textrm{si }\quad\left\{n \ge 0\,\vert\,X_n \in C\right\} \neq\emptyset,\\ +\infty& &\textrm{sinon.} \end{array} \right.
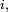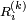  • L'instant de \scriptstyle\ k-ème retour en \scriptstyle\ i,\ noté \scriptstyle\ R^{(k)}_i\ et défini par récurrence par :
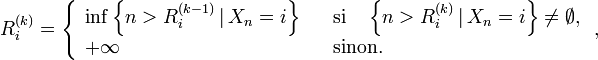
R^{(k)}_i = \left\{ \begin{array}{lll} \inf\left\{n > R^{(k-1)}_i\,\vert\,X_n = i\right\}& &\textrm{si }\quad\left\{n > R^{(k)}_i\,\vert\,X_n = i\right\} \neq\emptyset,\\ +\infty& &\textrm{sinon.} \end{array} \right.,
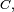ou encore l'instant de \scriptstyle\ k-ème entrée dans \scriptstyle\ C,\ sont des t.a..
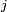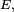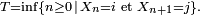  • Pour \scriptstyle\ i\ et \scriptstyle\ j\ dans \scriptstyle\ E,\ on pose \scriptstyle\ T = \inf\left\{n \ge 0\,\vert\,X_n = i \text{ et } X_{n+1} = j\right\}.\ On peut montrer que 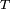\scriptstyle\ T \ n'est pas un temps d'arrêt, mais que, par contre, 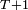\scriptstyle\ T + 1\ est un temps d'arrêt.


  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Temps d%27arr%C3%AAt ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Temps d'arret de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Temps d'arrêt — ● Temps d arrêt courte période pendant laquelle un mouvement, une opération sont suspendus …   Encyclopédie Universelle

  • Temps d'arrêt — Sommaire 1 Définitions 2 Interprétation 3 Notations 4 Propriétés 5 Exemples et contrexe …   Wikipédia en Français

  • temps d'arrêt — prastovos trukmė statusas T sritis automatika atitikmenys: angl. dead time; down time; downtime; fault time vok. Ausfallzeit, f; Stillstandszeit, f; Störungszeit, f; Totzeit, f rus. время простоя, n; простой, m pranc. temps d arrêt, m; temps de… …   Automatikos terminų žodynas

  • temps d’arrêt — prastovos trukmė statusas T sritis fizika atitikmenys: angl. down time; shut down time vok. Ausfallzeit, f; Leerlaufzeit, f; Stillstandzeit, f rus. время простоя, n pranc. durée d’indisponibilité, f; temps d’arrêt, m …   Fizikos terminų žodynas

  • Marquer une pause, un temps d'arrêt — ● Marquer une pause, un temps d arrêt interrompre une action, un processus, une progression …   Encyclopédie Universelle

  • non-uniformité du temps d'arrêt de groupe — grupinio vėlinimo trukmės netolygumas statusas T sritis radioelektronika atitikmenys: angl. group delay time nonuniformity vok. Gruppenlaufzeitungleichmäßigkeit, f rus. неравномерность времени групповой задержки, f pranc. non uniformité du temps… …   Radioelektronikos terminų žodynas

  • arrêt — [ arɛ ] n. m. • arest 1175; de arrêter A ♦ 1 ♦ Action d arrêter ou de s arrêter (dans sa marche, son mouvement); état de ce qui n est plus en mouvement. L arrêt d un train en gare; des autobus aux stations. Cinq minutes d arrêt. Arrêt accidentel …   Encyclopédie Universelle

  • TEMPS — Chacun sait à quel aspect de son expérience répond le mot de temps; mais aucune définition de la notion correspondante n’a reçu jusqu’ici, chez les savants comme chez les philosophes, une approbation unanime. Sensible à cette difficulté qu’il… …   Encyclopédie Universelle

  • Temps d'immobilisation — Le temps d’arrêt ou d’immobilisation d’une machine, d’un appareil ou d’un service est le pourcentage de temps pendant lequel il a été hors service ou inactif sur une période donnée. Ce document provient de « Temps d%27immobilisation ». Catégorie  …   Wikipédia en Français

  • ARRÊT — s. m. Jugement d une cour, d une justice souveraine, par lequel une question de fait ou de droit est décidée. Arrêt de la cour royale, de la cour de cassation. Arrêt interlocutoire. Arrêt par défaut. Arrêt définitif. Arrêt contradictoire. Arrêt… …   Dictionnaire de l'Academie Francaise, 7eme edition (1835)

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”