Tas de sable

Les terrils (comme celui de Siegen, ci-dessus), quoiqu'artificiels, illustrent la notion de talus naturel : les particules trouvent en effet leur équilibre entre l'action de la gravité et le frottement intergranulaire.

La notion de talus naturel intervient en géologie, géomorphologie et en mécanique des sols pour décrire le comportement mécanique des sols pulvérulents.

Un constat empirique

Lorsqu'un matériau pulvérulent (sable, graviers, blocs rocheux, mais aussi limaille métallique, farine, sucre en poudre, etc.) se dépose gravitairement sur une surface restreinte, il tend à se former, lorsque suffisamment de grains sont déposés, en un tas conique. L'angle du cône est, dans une large mesure, une caractéristique:

• de la nature des particules (silice, sucre, métal, etc.)
• et de la géométrie des particules (sphères, sphéroïdes, polyèdres convexes, polyèdres étoilés, grains concassés)

En répétant plusieurs fois l'expérience avec le même matériau, l'angle est à peu près constant ; cet angle est appelé angle de talus naturel et plus spécifiquement angle de talus naturel des terres pour les terrains.

L'interprétation classique

Schéma statique pour l'équilibre d'une particule à la surface d'un empilement granulaire conique.

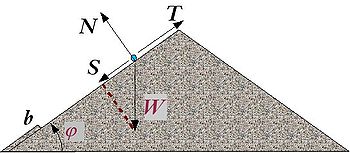
Dans cette interprétation, chaque grain du tas se dépose sans vitesse initiale. On procède à l'analyse de l'équilibre d'une particule, ou d'un grain, déposé sur la surface libre. On note φ l'angle que cette surface libre fait avec l'horizontale. Ce grain est soumis :

• à son poids 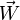, dont la composante active 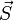tend à faire glisser la particule sur la surface ; le schéma montre que

  S = W× sin φ ;

• au frottement des particules du talus, qui se traduit par une force 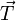, parallèle au talus et s'opposant à S ;

Les lois de la mécanique permettent de déterminer les intensités de ces différentes forces :

• d'après la loi des actions réciproques,

  N + W×cos φ = 0

• d'après la loi de frottement de Coulomb (loi du frottement sec), le frottement possède une intensité T comprise entre 0 et μ×N, où μ est le coefficient de frottement statique inter-grains (μ est compris entre 0 et 1 en général) ;
• enfin, l'équilibre de la particule s'écrit
  
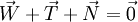
  (principe fondamental de la statique), soit, en projection sur la surface du talus :

  S + T = 0.

La combinaison de ces relations donne :

W×sin φ + T = 0, avec - μ×W×cos φ < T < 0.

• Si tan φ ≤ μ, alors T = -W×sin φ ;
• si en revanche tan φ > μ, alors T = -μ×W×cos φ mais l'équilibre est rompu, car S surpasse T et la particule glisse le long du talus, jusqu'à ce qu'elle soit interceptée par des particules ayant précédemment glissé, disons au point b : elle forme alors une nouvelle couche du talus, parallèle à la précédente.

Les particules sur la surface du talus sont donc en réalité des particules qui ont glissé et ont butté sur les particules inférieures. Elles subissent juste avant leur butée à une force

.

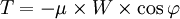Cette remarque permet d'identifier l'angle φ du talus : puisque

,

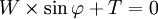par conséquent

.

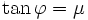Ainsi, la théorie classique identifie l'angle de talus et l'angle de frottement intergranulaire.

Applications du concept

L'angle de talus naturel, assimilé à l'angle de frottement intergranulaire, intervient dans toute application relative aux poudres ou aux matériaux pulvérulents en général :

• profil à donner aux remblais (fortifications anciennes)
• calcul des silos de stockage des grains,
• frittage des poudres métalliques en métallurgie,
• murs de soutènement et rideaux de palplanches,
• transporteurs à secousse

Limites du concept

L'analyse classique ne peut donner qu'un ordre d'idée de l'angle de frottement intergranulaire, pour les raisons suivantes :

• elle suppose que l'équilibre du talus est indifférent à la géométrie des grains. Cela peut se justifier en considérant que les grains sont de géométrie très hétérogène et qu'après tout, si l'angle de talus intègre une information sur l'interaction géométrique, cela suffira pour dimensionner des structures. Mais en pratique, l'industrie utilise bien souvent des matériaux présentant une homogénéité de géométrie ; or on observe bien une différence de comportement entre grains «roulés» (galets) et grains anguleux («concassés»), et il est intéressant de pouvoir en tenir compte a priori.
• d'autre part, un empilement a, au moins initialement, une structure lâche, et le talus se tasse sous son propre poids au fil du temps : l'indice des vides diminue, ce qui augmente l'angle de frottement apparent (loi de Caquot). Aussi l'échelle de mesure (c'est-à-dire la hauteur du tas considéré) de l'angle de talus n'est-elle pas indifférente.
• Dans le cas de graines végétales, il se produit aussi un écrasement d'une partie de l'effectif des grains, les grains de la base du tas n'étant pas homogène à ceux du haut du silo.

Historique

La notion de talus naturel présente un intérêt historique car elle montre comment les ingénieurs ont tenté de relier des grandeurs géométriques, donc observables et mesurables (un angle, une hauteur de remblai) à des notions de force. L'analyse d'empilements granulaires apparaît dans l'Architecture Hydraulique de Bélidor, où l'auteur considère l'équilibre de grains pris individuellement. Ces idées seront développées par Pierre-Antoine Couplet dans deux articles de Histoire de l'Académie royale des sciences (1726 et 1728) : Mémoire sur la poussée des terres et la résistance des revêtements. Les ingénieurs du Génie militaire : Coulomb, puis Poncelet, feront le plus grand usage de la notion d'angle de frottement (assimilé peu ou prou à l'angle de talus naturel).

Liens externes

• Conférence Physique des tas de sable et de la matière molle par Etienne Guyon à l'Université de tous les savoirs

Bibliographie

• André Guillerme - Bâtir la ville (1995), éd. Champs-Vallon, 124 p. ISBN 2-87673-203-3
• M. Reimbert et A. Reimbert, Détermination et interprétation des équilibres de poussée et de butée d'un massif pulvérulent (Juillet-août 1965), Annales de l'ITBTP, Série Sols et Fondations n°52, p. 1051

• Portail des sciences de la Terre et de l’Univers