Table de karnaugh

Cet article explique ce qu'est un tableau de Karnaugh, seulement dans une application logique binaire. Cet article n'explique pas les principes de base de la logique. Pour cela, voir l'article Fonctions logiques.

Un tableau de Karnaugh sert à simplifier des équations logiques ou à trouver l'équation logique correspondant à une table de vérité. La méthode utilisée est graphique et simple. Elle utilise également le Code de Gray ou binaire réfléchi, qui a comme propriété principale de ne faire varier qu'un seul bit entre deux mots successifs. La variation d'un seul bit est appelé distance de Hamming. A chaque variation d'un bit,il faut s'assurer que dH=1.

Sommaire 1 Principe 2 Méthode de recherche de l'équation 2.1 La somme 2.2 Le Produit 2.3 Utilisation 3 Voir aussi 4 Liens externes : simulateurs de table de Karnaugh

Principe

Le tableau de Karnaugh est un tableau étudié pour pouvoir trouver la plus simple équation d'une table de vérité. Elle se présente comme ceci :

Tableau de Karnaugh

S	CD		00		01		11		10
AB
00			0		1		1		0
01			0		1		1		1
11			0		1		1		1
10			0		1		1		0

Bien sûr, il peut y avoir plus ou moins de 4 variables (Ici A, B, C et D).

• La colonne 1 correspond aux valeurs de S pour C=0 et D=0
• La colonne 2 correspond aux valeurs de S pour C=0 et D=1
• La colonne 3 correspond aux valeurs de S pour C=1 et D=1
• La colonne 4 correspond aux valeurs de S pour C=1 et D=0

• La ligne 1 correspond aux valeurs de S pour A=0 et B=0
• La ligne 2 correspond aux valeurs de S pour A=0 et B=1
• La ligne 3 correspond aux valeurs de S pour A=1 et B=1
• La ligne 4 correspond aux valeurs de S pour A=1 et B=0

Ainsi, la case de la colonne 2 de la ligne 4 correspond à la valeur de S pour laquelle A=1, B=0, C=0 et D=1. Sa valeur peut-être trouvée dans la table de vérité ou par une équation à simplifier. On remplit de cette manière le tableau de Karnaugh.

Les valeurs du tableau de Karnaugh correspondent aux valeurs de la table de vérité suivante :

Table de vérité

A	B	C	D		S
0	0	0	0		0
0	0	0	1		1
0	0	1	0		0
0	0	1	1		1
0	1	0	0		0
0	1	0	1		1
0	1	1	0		1
0	1	1	1		1
1	0	0	0		0
1	0	0	1		1
1	0	1	0		0
1	0	1	1		1
1	1	0	0		0
1	1	0	1		1
1	1	1	0		1
1	1	1	1		1

Méthode de recherche de l'équation

Pour trouver l'équation de S, c'est simple. Il y a deux méthodes :

• Former une somme
• Former un produit

La somme

Pour trouver une somme, il faut regrouper les valeurs de S égales à 1. Le nombre de 1 dans chaque groupe doit être un nombre paire. Les groupes formés doivent être les moins nombreux possibles, mais ils doivent englober tous les 1. Un 1 peut être inclus dans plus d'un groupe, par contre aucun 0 ne doit être inclus. Les groupes sont composés d'une ou plusieurs colonnes et d'une ou plusieurs lignes. Si possible, assemblez-les par valeurs d'entrées communes. Par exemple, la colonne 2 et la colonne 3 ont pour valeur commune D=1. La ligne 1 et la ligne 4 ont la valeur B=0 en commun;

Pour les tables à 4 variables, de préférence procéder dans l'ordre suivant :

• Le rectangle 16 cases puis,
• les rectangles 8 cases puis,

• les rectangles 4 cases puis,
• les rectangles 2 cases et,
• enfin les cases uniques.

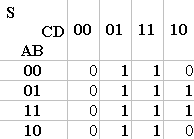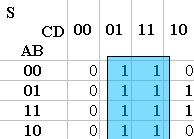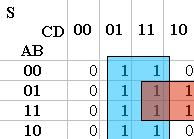
Dans l'exemple pris ci-dessus : on peut former un rectangle de 8 cases, puis un carré de 4 (le rectangle des colonnes 2 et 3 et le carré au croisement des lignes 2-3 et des colonnes 3-4). Le rectangle correspond à l'équation « D » car dans ces deux colonnes et dans ces deux colonnes seulement, D est toujours égal à 1 et, dans ces deux colonnes uniquement. Le carré correspond à l'équation « B·C » car dans ces cases et dans ces cases seulement B=1 et C=1. On fait ensuite la somme des deux équations et on obtient pour équation de S : « S = D + B·C ».

Cette méthode, une fois assimilée, permet de trouver une équation au premier coup d'œil, et propose une alternative simple à la simplification d'équation, qui peut rapidement devenir fastidieuse.

Le Produit

Cette méthode a pour but non pas de regrouper les « 1 » mais les « 0 », pour trouver non pas une somme de produits mais un produit de sommes.

TD4 : Formes conjonctives

Utilisation

Les tables/tableaux de Karnaugh sont surtout utilisé(e)s en électronique. En effet, la simplification de l'expression algébrique booléenne permet d'économiser des opérateurs logiques (portes logiques) et donc des circuits. Elle engendre aussi une économie de temps de conception et de fonds, tout en augmentant la fiabilité de l'ensemble.

En programmation, l'utilisation des tables de Karnaugh permet de réduire les séquences de conditions de test complexes en les regroupant en des conditions non intuitives au premier abord, mais qui réduisent la complexité effective du code (volume du source), ainsi que son temps d'exécution en réduisant le nombre des évaluations nécessaires.

Voir aussi

• Système binaire
• Électronique numérique
• Algèbre de Boole

Liens externes : simulateurs de table de Karnaugh

• Solveur : http://k-map.sourceforge.net

• Portail de la logique
• Portail des mathématiques