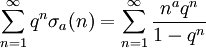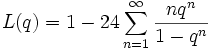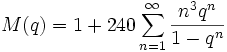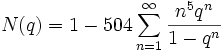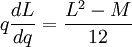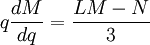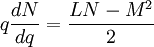- Séries d'Eisenstein
-
Série d'Eisenstein
En mathématiques, les séries d'Eisenstein désignent certaines formes modulaires dont le développement en série de Fourier peut s'écrire explicitement.
Sommaire
Séries d'Eisenstein du groupe modulaire
Pour un nombre complexe τ de partie imaginaire strictement positive, on définit la série d'Eisenstein G2k(τ) pour chaque entier k > 1 comme :
C'est remarquable, la série d'Eisenstein est une forme modulaire. Explicitement, si
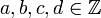 avec ad − bc = 1 alors :
avec ad − bc = 1 alors :Donc, G2k est une forme modulaire de poids 2k.
Relations de récurrence
Toute forme modulaire holomorphe pour le groupe modulaire peut être écrite comme polynôme en G4 et G6.
Soit dk = (2k + 3)k!G2k + 4. On dispose de la relation :
Ici,
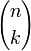 est le coefficient binomial et d0 = 3G4 et d1 = 5G6.
est le coefficient binomial et d0 = 3G4 et d1 = 5G6.Les dk apparaissent dans l'expansion en séries entières de la fonction de Weirstrass :
Séries de Fourier
Posons q = e2πiτ. Alors les séries de Fourier des séries d'Eisenstein sont :
où les coefficients de Fourier c2k sont donnés par :
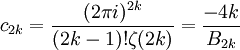 .
.
Ici, les Bn sont les nombres de Bernoulli, ζ(z) est la fonction de Riemann et σp(n) est simplement la somme des p-ièmes puissances des diviseurs de n.
La sommation sur q se résume à la série de Lambert :
Pour un nombre complexe q de module <1.
Identités de Ramanujan
Ramanujan a donné de nombreuses identités intéressantes entre les tous premiers termes.
Alors :
- Portail des mathématiques
Catégorie : Série
Wikimedia Foundation. 2010.

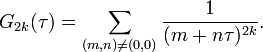
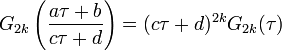
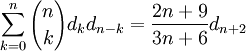
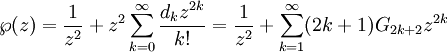
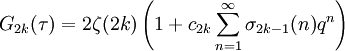
![G_4(\tau)=\frac{\pi^4}{45} \left[ 1+ 240\sum_{n=1}^\infty \sigma_3(n) q^{n} \right]](/pictures/frwiki/51/3f8388e69210a1f70d3e59c024761491.png)
![G_6(\tau)=\frac{2\pi^6}{945} \left[ 1- 504\sum_{n=1}^\infty \sigma_5(n) q^{n} \right]](/pictures/frwiki/54/6bc500c1f56a91947b3debef65c57bd1.png)