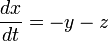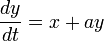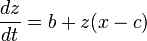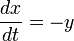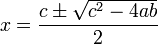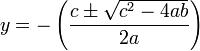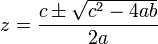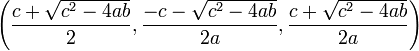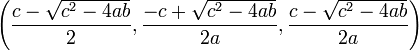Système de Rossler

Attracteur de Rössler

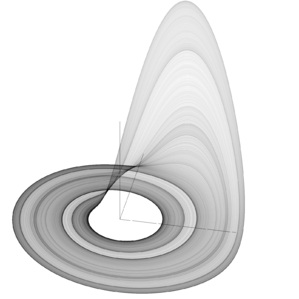
L'attracteur de Rössler

L'attracteur de Rössler est l'attracteur associé au système dynamique de Rössler, un système de 3 équations différentielles non-linéaires.

Ces équations différentielles définissent un système dynamique continu et tridimensionnel qui présente des caractéristiques chaotiques. L'ensemble des trajectoires à long terme de ce système définissent un attracteur étrange aux propriétés fractales.

Sommaire

1 Historique
2 Le système de Rössler
3 Propriétés
4 Bibliographie
5 Voir aussi
- 5.1 Articles connexes
- 5.2 Liens externes

Historique

Otto Rössler conçut son attracteur en 1976 dans un but purement théorique, mais ces équations s'avérèrent utiles dans la modélisation de l'équilibre dans les réactions chimiques. L'article original de Rössler mentionne que son système a été conçu pour fonctionner d'une façon similaire au système de Lorenz, mais également pour être plus simple à analyser, il ne présente qu'une seule spirale.

Le système de Rössler

Les équations de ce système sont:

$\frac{dx}{dt} = -y - z$

$\frac{dy}{dt} = x + ay$

$\frac{dz}{dt} = b + z(x-c)$

Rössler étudia l'attracteur pour $a = 0,2$ , $b = 0,2$ , et $c = 5,7$ , mais les propriétés de $a = 0,1$ , $b = 0,1$ , et $c = 14$ sont aujourd'hui plus étudiées.

Propriétés

Certaines propriétés du système de Rössler sont déduites par des méthodes linéaires et des vecteurs propres, mais les caractéristiques principales de ce système requiert des méthodes non-linéaires comme les sections de Poincaré ou les diagrammes de bifurcation.

Une orbite dans l'attracteur suit une spirale proche du plan $x, y$ autour d'un point fixe instable. S'éloignant progressivement de ce point fixe, un second point fixe provoque une élévation de cette orbite et une redescente vers le plan $x, y$ proche du premier point fixe, réintégrant l'orbite dans la spirale.

Bien que les valeurs des différentes variables soient bornées, il est apparent que ces oscillations sont chaotiques.

Vue depuis le plan x,y

L'un des intérêts de l'attracteur de Rössler est le caractère linéaire de deux de ses équations. Poser $z = 0$ , permet l'examen de sa projection dans le plan $x, y$ :

$\frac{dx}{dt} = -y$

$\frac{dy}{dt} = x + ay$

Points fixes

Pour trouver les points fixes, les trois équations de Rössler sont posées égales à zéro. Le système est alors résolu et donne le résultat suivant:

$x = \frac{c\pm\sqrt{c^2-4ab}}{2}$

$y = -\left(\frac{c\pm\sqrt{c^2-4ab}}{2a}\right)$

$z = \frac{c\pm\sqrt{c^2-4ab}}{2a}$

Ce qui, maintenant, peut être utilisé pour présenter les points fixes pour des valeurs données de paramètres :

$\left(\frac{c+\sqrt{c^2-4ab}}{2}, \frac{-c-\sqrt{c^2-4ab}}{2a}, \frac{c+\sqrt{c^2-4ab}}{2a}\right)$

$\left(\frac{c-\sqrt{c^2-4ab}}{2}, \frac{-c+\sqrt{c^2-4ab}}{2a}, \frac{c-\sqrt{c^2-4ab}}{2a}\right)$

Comme cité plus haut, l'un des points, instable, est situé au centre de la spirale et l'autre se situe hors de l'attracteur.

Régimes périodiques et chaotiques

Posant a = 0,1 et b = 0,1 et en faisant varier le paramètre c, le système passe successivement par divers régimes périodiques ou chaotiques:

$c = 4$ ⇒ période 1
$c = 6$ ⇒ période 2
$c = 8,5$ ⇒ période 4
$c = 9$ ⇒ chaotique
$c = 12$ ⇒ période 3
$c = 12,6$ ⇒ période 6
$c = 13$ ⇒ chaotique
$c = 18$ ⇒ chaotique

Bibliographie

E. N. Lorenz, « Deterministic nonperiodic flow », dans J. Atmos. Sci., vol. 20, 1963, p. 130–141 [lien DOI]
O. E. Rössler, « An Equation for Continuous Chaos », dans Physics Letters, vol. 57A, n^o 5, 1976, p. 397–398
O. E. Rössler, « An Equation for Hyperchaos », dans Physics Letters, vol. 71A, n^o 2,3, 1979, p. 155–157
(en) Steven H. Strogatz, Nonlinear Dynamics and Chaos, Perseus publishing, 1994

Voir aussi

Liens externes

Animation Flash avec PovRay
Attracteurs de Rössler et de Lorenz - animation java
Attracteur 3D dynamique

Ce document provient de « Attracteur de R%C3%B6ssler ».

Catégorie : Théorie du chaos

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Système de Rossler de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Système de rössler — Attracteur de Rössler L attracteur de Rössler L attracteur de Rössler est l attracteur associé au système dynamique de Rössler, un système de 3 équations différentielles non linéaires. Ces équations différentielles définissent un système… … Wikipédia en Français
Rössler Weiher — Vorlage:Infobox Fluss/BILD fehltVorlage:Infobox Fluss/QUELLHÖHE fehltVorlage:Infobox Fluss/MÜNDUNG fehltVorlage:Infobox Fluss/MÜNDUNGSHÖHE fehltVorlage:Infobox Fluss/HÖHENUNTERSCHIED fehltVorlage:Infobox Fluss/EINZUGSGEBIET fehltVorlage:Infobox… … Deutsch Wikipedia
Attracteur de Rossler — Attracteur de Rössler L attracteur de Rössler L attracteur de Rössler est l attracteur associé au système dynamique de Rössler, un système de 3 équations différentielles non linéaires. Ces équations différentielles définissent un système… … Wikipédia en Français
Attracteur de Rössler — L attracteur de Rössler L attracteur de Rössler est l attracteur associé au système dynamique de Rössler, un système de 3 équations différentielles non linéaires. Ces équations différentielles définissent un système dynamique continu et… … Wikipédia en Français
Otto Rössler — Otto E. Rössler, né le 20 mai 1940 à Berlin, est un biochimiste allemand et scientifique pluridisciplinaire d exception notamment dans le chaos. Sommaire 1 Biographie 2 Références 3 Bibliography … Wikipédia en Français
Chaos-Theorie — Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den… … Deutsch Wikipedia
Chaos Theorie — Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den… … Deutsch Wikipedia
Chaosphysik — Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den… … Deutsch Wikipedia
Chaostheoretiker — Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den… … Deutsch Wikipedia
Chaostheorie — Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den… … Deutsch Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Système de Rossler

Attracteur de Rössler

Sommaire

Historique

Le système de Rössler