Systeme modulaire de representation : RNS

Systeme modulaire de representation : RNS

Système modulaire de représentation

En mathématiques, dans la branche de l'arithmétique modulaire, un système modulaire de représentation est un outil utilisé en cryptographie. Les systèmes modulaires de représentation des nombres (Residue Number System) sont une application du théorème des restes chinois. Les nombres sont représentés par leurs restes modulo un ensemble de valeurs premières entre elles. On peut définir une addition et une multiplication qui vont ainsi s'effectuer sur chaque module de façon indépendante.

Il est ainsi possible d'avoir des calculs parallèles sans propagation de retenues.

Sommaire

Définitions

Soit 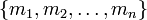\{m_1,m_2,\ldots,m_n\} un ensemble de modules mutuellement premiers entre eux. On l'appelle la base RNS.

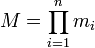
On note M=\prod_{i=1}^n m_i

Soit X un entier positif inférieur à M avec 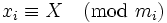x_i \equiv X\pmod{m_i}. La famille 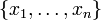\{x_1,\ldots,x_n\} est appelée représentation RNS de X.

D'après le théorème des restes chinois, la représentation RNS de chaque entier positif X inférieur à M est unique.

Opérations

Addition et multiplication

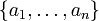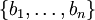Soit A et B deux entiers naturels positifs de représentations respectives \{a_1,\ldots,a_n\} et \{b_1,\ldots,b_n\}. Sur l'ensemble des nombres en représentation RNS, on peut définir les opérations suivantes :

L'addition : A + B est représenté par l'ensemble des ai + bi pour chaque module mi

La multiplication : 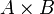A\times B est représenté par l'ensemble des a_i\times b_i pour chaque module mi.

Division

La définition d'une division est plus problématique.

Ce document provient de « Syst%C3%A8me modulaire de repr%C3%A9sentation ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Systeme modulaire de representation : RNS de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Système modulaire de représentation : RNS — Système modulaire de représentation En mathématiques, dans la branche de l arithmétique modulaire, un système modulaire de représentation est un outil utilisé en cryptographie. Les systèmes modulaires de représentation des nombres (Residue Number …   Wikipédia en Français

  • Système modulaire de représentation : rns — Système modulaire de représentation En mathématiques, dans la branche de l arithmétique modulaire, un système modulaire de représentation est un outil utilisé en cryptographie. Les systèmes modulaires de représentation des nombres (Residue Number …   Wikipédia en Français

  • Système modulaire de représentation — En mathématiques, dans la branche de l arithmétique modulaire, un système modulaire de représentation est un outil utilisé en cryptographie. Les systèmes modulaires de représentation des nombres (Residue Number System) sont une application du… …   Wikipédia en Français

  • Systeme de numeration — Système de numération Numérations selon les cultures Numération arabo indienne arabe khmer indienne mongole thaï Numérations à l’origine chinoise chinoise japonaise à bâtons suzhou Numérations alphabétiques …   Wikipédia en Français

  • Système numéral — Système de numération Numérations selon les cultures Numération arabo indienne arabe khmer indienne mongole thaï Numérations à l’origine chinoise chinoise japonaise à bâtons suzhou Numérations alphabétiques …   Wikipédia en Français

  • Système de numération — Un système de numération est un ensemble de règles d utilisation des signes, des mots ou des gestes permettant d écrire, d énoncer ou de mimer des nombres. Sous leur forme écrite, ces derniers sont nés, en même temps que l écriture, de la… …   Wikipédia en Français

  • RNS — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.   Sigles d’une seule lettre   Sigles de deux lettres > Sigles de trois lettres   Sigles de quatre lettres …   Wikipédia en Français

  • Systèmes de numération — Système de numération Numérations selon les cultures Numération arabo indienne arabe khmer indienne mongole thaï Numérations à l’origine chinoise chinoise japonaise à bâtons suzhou Numérations alphabétiques …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”