Sextants

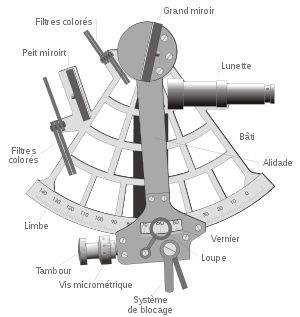
Sextants

Sextant

Page d'aide sur l'homonymie Pour les articles homonymes, voir Sextant (homonymie).
Un sextant.

Un sextant est un instrument de navigation permettant de relever la hauteur angulaire d’un astre au-dessus de l’horizon. Il est utilisé pour faire le point hors de vue de terre (voir l’article : navigation astronomique). Un usage courant du sextant est de relever la hauteur angulaire du soleil à midi, ce qui donne la latitude du point de l'observateur. Le sextant est toujours utilisé dans l’aéronautique, la marine, les raids terrestres, etc., bien que son usage se restreigne en raison du développement des systèmes de positionnement par satellites.

Sommaire

Histoire

Les grecs antiques et byzantins utilisaient déjà pour la navigation des astrolabes et des octants, tels ceux trouvés à Anticythère dans une épave du IIIe siècle av. J.-C.; Héron d’Alexandrie (Ier siècle) en fait la description.

Toutefois, le sextant moderne fut inventé dans les années 1730 par deux personnes indépendamment l’une de l’autre: John Hadley (1682-1744), un mathématicien anglais, et Thomas Godfrey (1704-1749), un inventeur américain.

La spécificité du sextant par rapport à l’astrolabe est que les deux directions dont on veut mesurer l’angle sont observées en même temps, rendant la mesure à peu près indépendante des mouvements du navire. Le sextant se tient à hauteur des yeux, alors que l’astrolabe nécessite un point de suspension d’autant plus élevé que l’on vise un astre de site élevé.

Précision des mesures et réglage

Schéma d’un sextant

La lecture d’un sextant bien réglé permet une précision de 0,2′ d’arc. En théorie, un observateur pourrait donc déterminer sa position avec une précision de 0,2 milles marins (puisque 1 mille correspond à 1′ d’arc de grand cercle), soit environ 370 mètres. Dans la pratique, les navigateurs obtiennent une précision de l’ordre de 1 ou 2 milles marins (mouvements du navire, houle, horizon plus ou moins net, imprécisions de l’heure ou de l’estime entre les visées successives du même astre ou d’astres différents).

Les erreurs instrumentales du sextant sont l’excentricité et la collimation.

  • l’excentricité est une donnée propre du sextant à la construction et ne peut être corrigée. Elle est fonction de la hauteur mesurée et est inscrite dans la boîte du sextant ;
  • la collimation peut être réglée et il y a lieu de la vérifier avant chaque observation en superposant l’image directe d’un astre et son image réfléchie et inversement, la collimation étant égale à la moyenne de ces deux mesures.

Si la collimation dépasse 3′, il faut vérifier et rectifier :

  • l’axe optique (vieux sextants), qui doit être parallèle au plan du limbe, en comparant les visées d’une mire à 30 m. par la lunette et par des cavaliers posés sur le limbe. On agit ensuite sur les vis de réglage du collier porte-lunette ;
  • le grand miroir, qui doit être, en comparant la visée directe d’un cavalier avec la visée réfléchie par le grand miroir d’un second cavalier. On agit ensuite sur la vis de réglage du grand miroir ;
  • le petit miroir, qui doit être perpendiculaire au plan du limbe et parallèle au grand miroir, en visant un point éloigné ou l’horizon : les deux images doivent être confondues et le rester en inclinant le sextant. On agit sur les vis de réglage du petit miroir.

Mesure de la hauteur d'un astre au sextant

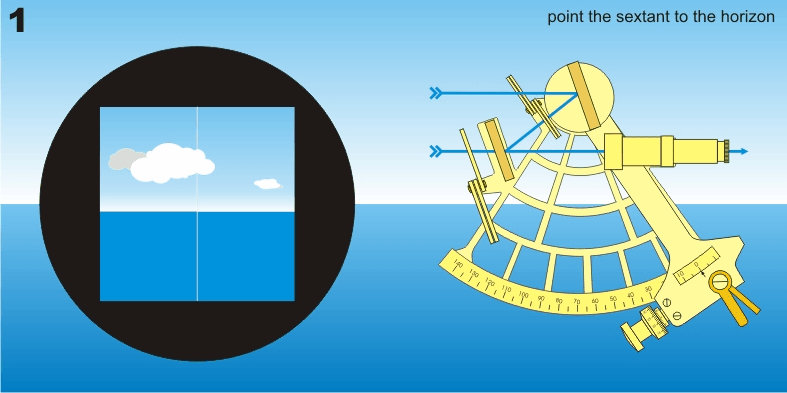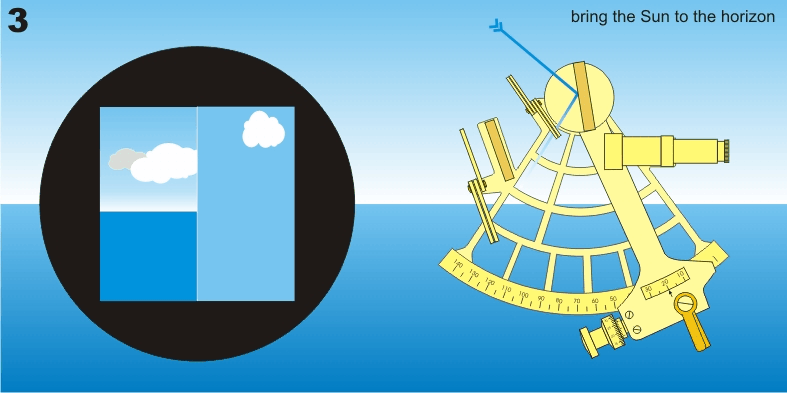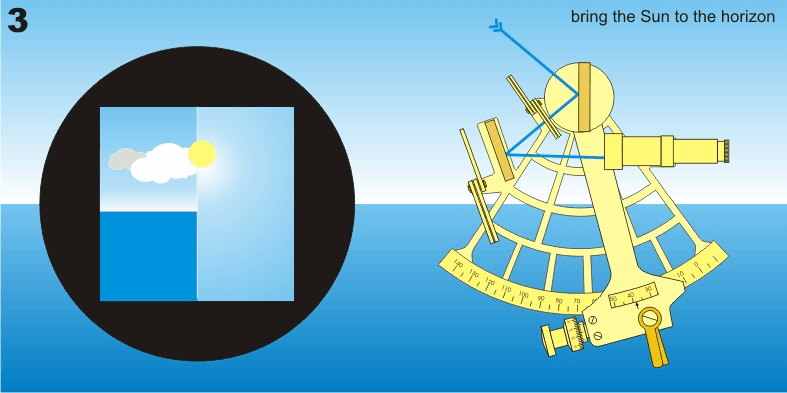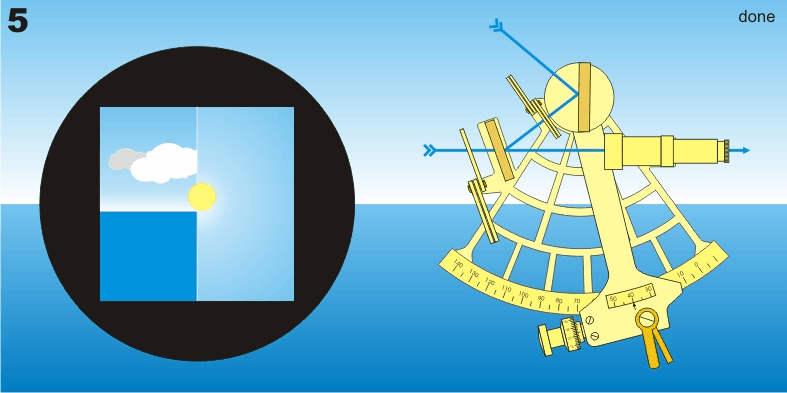
Mesure avec un sextant

L’observation consiste à « faire descendre » l’image réfléchie de l’astre sur l’horizon et la faire tangenter l’horizon (d’où le mouvement de balancier de la main qui tient le sextant). S’il s’agit du soleil ou de la lune, on fait tangenter son bord inférieur ou supérieur. Pour les étoiles et les planètes, il est conseillé de « monter l’horizon » au voisinage de l’astre en retournant le sextant, puis d’observer normalement.

La hauteur mesurée au sextant doit être corrigée des erreurs instrumentales et d’un certain nombre de paramètres propres à la hauteur de l’observateur au-dessus de l’eau, à la réfraction astronomique et à l’astre visé.

La hauteur vraie 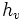h_v\, est déduite de la hauteur mesurée 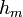h_m\, par la formule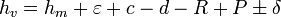

h_v = h_m + \varepsilon + c - d - R + P \pm\delta\,
avec :
\varepsilon\, , l’excentricité du sextant ;
c\, , la collimation du sextant ;
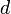d\, , la dépression de l’horizon, fonction de la hauteur de l’œil de l’observateur, donné par les éphémérides ;
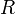R\, , la réfraction astronomique ;
P\, , la parallaxe (négligeable pour les étoiles et les planètes) ;
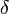\delta\, , le demi-diamètre (apparent) de la lune ou du soleil, affecté du signe + si on a visé le bord inférieur, du signe - si on a visé le bord supérieur.

Pour le soleil, les éphémérides donnent la valeur journalière de 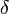\delta\, ainsi que la somme 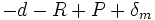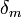- d - R + P + \delta_m\, ; \delta_m\, étant le demi-diamètre moyen et on applique une deuxième correction : 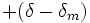+(\delta - \delta_m)\, pour le bord inférieur et 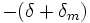-(\delta + \delta_m)\, pour le bord supérieur.

Pour la lune on applique une formule analogue avec des valeurs données par les éphémérides.

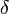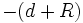Pour les étoiles et planètes : \delta\, est négligeable ; P\, est négligeable, sauf pour Mars et Vénus. La somme -(d + R)\, est fournie par les éphémérides ainsi que la valeur de P\, pour Mars et Vénus.

Autres usages

Distance d'un amer

On mesure au sextant la hauteur angulaire d’un amer dont on connaît la hauteur. Il convient toutefois d’être prudent :

  • l’édifice doit être complètement visible : il ne doit pas avoir les pieds dans l’eau et ne pas être en partie derrière l’horizon ;
  • il ne faut pas confondre la hauteur de l’édifice avec l’élévation du foyer d’un phare ou d’un feu, qui seule est mentionnée sur les cartes marines et comptée depuis le niveau des hautes mers de vives-eaux (coefficient 95).

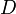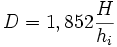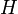La distance D\, en nautiques : D = 1,852 \frac{H}{h_i}\, avec H\, la hauteur de l’édifice en mètres et 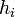h_i\, la hauteur instrumentale en minutes.

Angles horizontaux

En utilisant le sextant dans le plan horizontal, il est possible de mesurer l’angle entre deux objets. Cette méthode permet de faire un point par arcs capables ; voir l’article : Navigation côtière.

Voir aussi

Articles connexes

Liens externes

Sur les autres projets Wikimedia :

  • Portail du monde maritime Portail du monde maritime
  • Portail de l’astronomie Portail de l’astronomie
  • Portail de l’aéronautique Portail de l’aéronautique
Ce document provient de « Sextant ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sextants de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • sextants — sex·tant || sekstÉ™nt n. early navigational instrument for determining latitude and longitude by measuring angular distances …   English contemporary dictionary

  • Sextant — This article is about the sextant as used for navigation. For the astronomer s sextant, see Sextant (astronomical). : For the history and development of the sextant see Reflecting instruments A sextant is an instrument generally used to measure… …   Wikipedia

  • Reflecting instrument — Reflecting instruments are those that use mirrors to enhance their ability to make measurements. In particular, the use of mirrors permits one to observe two objects simultaneously while measuring the angular distance between the objects. While… …   Wikipedia

  • Sextant (astronomical) — This article is about the Sextant as used for astrometry. For the navigator s sextant, see Sextant . Sextants for astronomical observations were used primarily for measuring the positions of stars. They are little used today, having been replaced …   Wikipedia

  • Sextant — Pour les articles homonymes, voir Sextant (homonymie). Un sextant. Un sextant est un instrument de navigation à réflexion servant à mesurer la distance angulaire entre deux points aussi bien verticalement qu h …   Wikipédia en Français

  • Celestial navigation — Celestial navigation, also known as astronavigation, is a position fixing technique that was devised to help sailors cross the featureless oceans without having to rely on dead reckoning to enable them to strike land. Celestial navigation uses… …   Wikipedia

  • BaBar experiment — The BaBar experiment is an international collaboration of more than 550 physicists and engineers studying the subatomic world at energy of approximately ten times the rest mass of a proton. Its design was motivated by the investigation of CP… …   Wikipedia

  • Backstaff — Not to be confused with Ballastella. Davis quadrant from the beginning of the 18th century The backstaff or back quadrant is a navigational instrument that was used to measure the altitude of a celestial body, in particular the sun or moon. When… …   Wikipedia

  • Kelvin Hughes — is a major player in the design and manufacture of marine navigation systems and the supply of navigational data to both the merchant marine and naval marketplace. Navigational and tactical display systems from Kelvin Hughes are fitted to ships… …   Wikipedia

  • Lunar distance (navigation) — For the history of the lunar distance method, see History of longitude. Finding Greenwich time while at sea using a lunar distance. The Lunar Distance is the angle between the Moon and a star (or the Sun). The altitudes of the two bodies are used …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”