Résidu de Solow

Le modèle de Solow est un des principaux modèles de la théorie de la croissance économique. Développé par Robert Solow, il est un modèle de l'économie néoclassique.

Sommaire 1 Présentation 2 Expression mathématique 2.1 Fonction de production 2.2 Equation du PIB 2.3 Equation d'épargne 2.4 Equation d'évolution du capital 2.5 Evolution de la force de travail 3 Les enseignements du modèle 3.1 L'équilibre stationnaire 3.2 L'appauvrissement de l'économie 3.3 L'enrichissement de l'économie 4 Évolution du modèle 5 Notes et références 6 Bibliographie 7 Annexes 7.1 Articles connexes

Présentation

Robert Solow a construit un modèle formel de la croissance, à partir d'une réflexion critique sur le modèle de Harrod-Domar, qui constitue encore aujourd'hui le modèle de référence en science économique. Solow n'imaginait pas l'impact qu'aurait son modèle dans le contexte historique de l'époque de la Guerre Froide. Le modèle de Harrod était un modèle pessimiste qui pouvait être utilisé par les Marxistes pour annoncer la fin du Capitalisme. Le modèle de Solow est de nature optimiste car il ne prévoit pas de situation de crise. D'inspiration néo-classique, ce modèle se fonde sur une fonction de production à deux facteurs: le travail et le capital. La production résulte donc exclusivement de la mise en combinaison d'une certaine quantité de capital (capital physique) et de travail (main d'œuvre). Solow appartient à l'école de la Synthèse, son modèle se fera critiquer par les néoclassiques et les keynésiens.

Le modèle de Solow se fonde sur l'hypothèse que les facteurs de production connaissent des rendements décroissants, c'est-à-dire qu'une augmentation de ceux-ci dans une certaine proportion engendre une augmentation dans une proportion plus faible de la production. Il pose également comme hypothèse que les facteurs de production sont utilisés de manière efficace par tous les pays. En posant que la population connaît un taux de croissance que Solow qualifie de « naturel » (non influencé par l'économie), le modèle déduit trois prédictions :

1. Augmenter la quantité de capital (c’est-à-dire investir) augmente la croissance : avec un capital plus important, la main d'œuvre augmente sa productivité (dite apparente).
2. Les pays pauvres auront un taux de croissance plus élevé que les pays riches. Ils ont en effet accumulé moins de capital, et connaissent donc des rendements plus faiblement décroissants, c’est-à-dire que toute augmentation de capital y engendre une augmentation de la production proportionnellement plus forte que dans les pays riches.
3. En raison des rendements décroissants des facteurs de production, les économies vont atteindre un point où toute augmentation des facteurs de production n'engendrera plus d'augmentation de la production par tête. Ce point correspond à l'état stationnaire. Solow note toutefois que cette troisième prédiction est irréaliste : en fait, les économies n'atteignent jamais ce stade, en raison du progrès technique qui accroît la productivité des facteurs.

Autrement dit, pour Solow, sur le long terme, la croissance provient du progrès technique. Toutefois, ce progrès technique est exogène au modèle, c'est-à-dire qu'il ne l'explique pas mais le considère comme donné (telle une « manne tombée du ciel »).

Par ailleurs, ce modèle est construit sur des hypothèses simplificatrices. Ce qui amène Joan Robinson à ironiser sur le caractère peu réaliste de ces hypothèses en parlant du « royaume de Solowie »^[1].

Expression mathématique

Le modèle de Solow est basé sur cinq équations macroéconomiques:

• une fonction de production
• une équation comptable sur le PIB
• une équation d'épargne
• une équation d'évolution du capital
• une équation d'évolution de la force de travail

Fonction de production

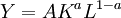
C'est une fonction de Cobb-Douglas où Y représente la production totale de l'économie, A la productivité globale des facteurs (aussi appelée niveau technologique ou niveau de progrès technique), K le capital et L le travail.

Equation du PIB

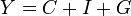
où C est la consommation des ménages, G les dépenses publiques et I l'investissement, égal à l'épargne.

Equation d'épargne

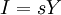
L'épargne (donc également l'investissement puisque I=S) est proportionnelle à Y, avec s la propension marginale à épargner.

Equation d'évolution du capital

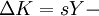
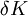
L’épargne est intégralement investie, ce qui accroît le stock de capital de l'économie, et par ailleurs le capital en place se déprécie, au rythme du taux de dépréciation du capital 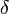(à chaque période, une part 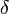du capital est ainsi perdue).

Evolution de la force de travail

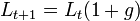
où g est le taux de croissance de la force de travail L.

Les enseignements du modèle

L'équilibre stationnaire

Le modèle de Solow est en équilibre stable, c'est-à-dire que toutes les économies convergeront vers un état d'équilibre de long terme. On parle d'« équilibre stationnaire ». Le seul déterminant de la vitesse de convergence est le taux d'épargne des agents économiques, s. Mathématiquement, les variables par tête n'évolueront plus ( notamment y et k), alors que les variables en niveau continueront d'évoluer à un taux n, le taux de croissance démographique.

Y_t = K_t = n,

Le premier enseignement que l'on peut tirer de cette formule est qu'une économie en état de croissance équilibrée voit son activité Y croître au même rythme que sa population n. Cela rejoint le modèle pessimiste de Harrod. En l'absence d'intervention publique, toutes les économies devraient converger à l'équilibre. La vérification empirique est contrastée: la Chine ou l'Irlande ont montré leur capacité à rattraper les économies occidentales, alors que d'autres économies comme les pays Africains ne décollent pas.

L'appauvrissement de l'économie

Le modèle de Solow met en évidence l'existence d'un lien entre un fort taux démographique et la pauvreté. En effet, une hausse de la démographie, toutes choses égales par ailleurs, entraine une diminution du capital par tête k, ce qui conduit à l'appauvrissement du pays. Cela rejoint l'idée de Malthus.

L'enrichissement de l'économie

D'autre part, une hausse du taux d'épargne s, toutes choses égales par ailleurs, entrainera une hausse du capital par tête k, et donc une hausse de la richesse y_t et Y_t

Évolution du modèle

Dans le prolongement du modèle de Solow, les modèles de croissance endogène ont été développés au cours des années 1980 pour répondre au problème de l'origine du progrès technologique, qui sera endogénéisé dans ces modèles.

Notes et références

Bibliographie

• Robert M. Solow, « A Contribution to the Theory of Economic Growth », dans Quarterly Journal of Economics, vol. 70, n^o 1, 1956, p. 65–94 [texte intégral] 

Annexes

Articles connexes

• Robert Solow
• Croissance économique

• Portail de l’économie