Règles de réécriture

En linguistique générative, les règles de réécriture, aussi appelées règles syntagmatiques, servent à créer des syntagmes ou des propositions. Cette notion a été introduite par Noam Chomsky dans le cadre de la théorie standard et constitue une réponse aux procédés distributionnels de Z.S. Harris et de L. Bloomfield pour qui la syntaxe est le résultat de la distribution de morphèmes dans la phrase.

Ce composant de la grammaire a la particularité d'engendrer des phrases de « haut en bas », c'est-à-dire en partant des éléments les plus abstraits pour aller vers des éléments plus concrets : les morphèmes.

L'autre avantage de ce type de grammaire est de simplifier la description d'un langage : par exemple, un syntagme nominal peut apparaître dans plusieurs positions dans une phrase (sujet, cod etc.) Alors qu'une grammaire à états finie devrait indiquer pour chaque position la règle de composition de cet élément, la grammaire à règles syntagmatiques ne doit spécifier qu'une seule fois la composition du syntagme nominal.

Principe

Une règle de réécriture est du type : X A Y → X Z Y, avec :

• X, Y, Z : symboles ou suite de symboles, avec éventuellement X et Y nuls.
• A : symbole unique non nul.

La manipulation d'une règle de réécriture consiste à remplacer un symbole unique par une suite non nulle distincte. Un élément est appelé initial s'il ne figure jamais à droite de la flèche et terminal s'il ne figure jamais à gauche de la flèche.

Dans les langues naturelles, le seul élément initial est P (pour phrase) alors que les éléments terminaux correspondent aux morphèmes. De plus, les éléments non terminaux comprennent les différentes catégories grammaticales.

Une suite de dérivations par règles de réécriture s'appelle un chaîne. Une chaîne est dite terminale lorsqu'aucune règle ne peut s'appliquer à aucun élément de cette chaîne.

Parmi les types de règles existantes, deux restent particulièrement importants :

• les règles context sensitive (en français : sensibles au contexte ou dépendantes du contexte) impliquent que X et Y ne sont pas tous les deux nuls.
• les règles context free (en français : règles indépendantes du contexte) impliquent X et Y nuls;

Formulation

Une règle de réécriture est formulée de la façon suivante :

• X → Y Z (se lit : X se réécrit Y Z)

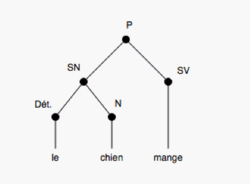
Exemples : soient les règles 1 et 2 :

• Règle 1 : P → SN SV
• Règle 2 : SN → Dét N

Et les variables :

• Dét = {le} ;
• N = {chien} ;
• SV = {mange} ;
• P = phrase

Application de la règle 2 sur la règle 1 :

(R1) : P → SN SV

⇔ (R2) : P → Dét N SV

Remplacement des variables :

P : le chien mange

Représentations

Représentation arborescente d'une chaîne de dérivations

Il existe plusieurs façons de représenter une chaîne de dérivations par règles de réécriture :

• l'arbre, correspondant à un type particulier de graphe mathématique (voir schéma) ;
• le parenthèsage étiqueté.

[_P [_SN [_Dét.le] [_Nchien] ] [_SVmange] ]

Références

• Nouveau dictionnaire encyclopédique des sciences du langage (1972), O. Ducrot et J.M. Schaeffer, Seuil, ISBN : 2-02-038181-8
• Introduction à la grammaire générative (1967), N. Ruwet, Plon.

• Portail de la linguistique