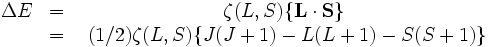Règle de multiplicité maximale

Règle de multiplicité maximale

Règle de Hund

En physique atomique, les règles de Hund se refèrent à un ensemble de règles simples utilisées pour déterminer quel est le terme spectroscopique fondamental de l'atome considéré. Elles furent proposées par Friedrich Hund. En chimie, la première de ces règles est particulièrement importante, et l'on se réfère souvent à elle seule sous le terme de « règle de Hund ».

Les trois règles de Hund sont :

  1. Pour une configuration électronique donnée, le terme de plus faible énergie est celui maximisant le spin total ( 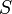S \, maximal).
  2. Pour un spin total donné, le terme de plus faible énergie est celui de plus grande valeur de 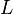L \, (moment cinétique orbital total).
  3. Pour un terme spectroscopique donné, dans un atome ayant sa couche externe à moitié pleine ou moins, le niveau de plus faible énergie est celui minimisant 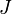J \, (nombre quantique lié au couplage spin-orbite). Dans un atome ayant sa couche externe plus qu'à moitié pleine, le niveau de plus faible énergie est celui de 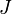J \, le plus élevé.

Ces règles montrent comment trouver de manière simple le terme spectroscopique fondamental. Elles supposent que le couplage spin-orbite est négligeable devant la répulsion des électrons de la couche externe, mais qu'il est aussi dominant par rapport à toutes les autres interactions non prises en compte. On parle alors de régime de couplage spin-orbite.

Les orbitales pleines ou les orbitales vides ne contribuent ni au spin total S, ni au moment cinétique orbitalaire total L. On peut montrer que dans ces cas là, le terme électrostatique résiduel (dû à la répulsion électronique) et le couplage spin-orbite, ne peuvent que déplacer en bloc tous les niveaux d'énergie. De ce fait, on ne considère en général que les électrons de valence pour ordonner les niveaux d'énergie.

Sommaire

Règle 1

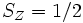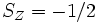En raison du principe d'exclusion de Pauli, 2 électrons ne peuvent partager les mêmes nombres quantiques dans le même système. Ainsi, chaque orbitale spatiale ne peut abriter que 2 électrons, de spin opposé (respectivement un spin selon une direction arbitraire Z de S_Z = 1/2 \, et S_Z = -1/2 \, ). La première règle de Hund stipule que le plus bas niveau en énergie est celui maximisant la valeur de S, somme des spin respectifs de chaque électron se trouvant dans les orbitales de valence de l'atome. Ainsi, chaque orbitale est d'abord occupée par un seul électron, ayant tous le même spin, jusqu'à ce qu'apparaissent nécessairement des paires.

Deux explications physiques ont été offertes (voir Levine p.303-4) pour la stabilité accrue des états de plus haute multiplicité. Aux premier jours de la mécanique quantique, on a proposé que les électrons aux orbitales différentes sont plus éloignés les uns des autres, de sorte que l'énergie de répulsion entre électrons est réduite. Cependant cette explication est maintenant périmée. Des calculs précis basés sur la mécanique quantique à partir des années 1970 démontrent plutôt que les électrons aux orbitales simplement occupés sont moins écrantés vis-à-vis du noyau, de sorte que ces orbitales se rétrécissent et l'énergie d'attraction entre électrons et noyau est augmentée.

Exemple

Considérons l'état fondamental de l'atome de silicium. La configuration électronique de Si est : 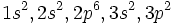1s^2, 2s^2, 2p^6, 3s^2, 3p^2 \, . Il nous faut considérer seulement les électrons 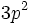3p^2 \, , pour lesquels on peut montrer que les termes spectroscopiques possibles sont 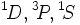{}^1\!D ,{}^3\!P ,{}^1\!S . La première règle de Hund dit alors que le terme d'énergie la plus basse est 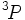{}^3\!P \, qui correspond à S = 1 \, .

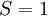Règle 2

Cette règle vise aussi à minimiser l'énergie de répulsion entre électrons. Elle peut être comprise en utilisant l'analogie classique suivante : si tous les électrons orbitent dans une même direction (celle de moment cinétique orbitalaire le plus élevé), ils se rencontrent moins souvent que si certains d'entre eux orbitent dans des directions opposées. Dans ce cas la force de répulsion électrostatique augmente, ce qui sépare les électrons, ajoutant une énergie potentielle répulsive, et donc augmentant l'énergie.

Exemple

Pour le silicium, il n'y a pas de choix de l'état triplet de spin 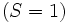(S = 1) \, . La seconde règle n'est donc pas utile. L'atome le plus léger requérant cette règle pour déterminer son terme de plus basse énergie est le titane (Ti, Z = 22) de configuration électronique 1s2 2s2 2p6 3s2 3p6 4s2 3d2. Cela conduit à 5 termes spectroscopiques dont 3 singulets (1S, 1D, et 1G) et 2 triplets (3P et 3F). On déduit de la première règle que le terme fondamental est un des deux triplets, et de la seconde règle que le terme fondamental est 3F (avec L = 3) plutôt que 3P (avec L = 1).

Règle 3

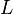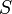Cette règle prend en compte les différences d'énergie liées au couplage spin-orbite. Dans le cas où le couplage est faible devant les répulsions électrostatiques des électrons, L \, et S \, restent des nombres quantiques utilisables et la différence d'énergie est donnée par :

\begin{matrix} \Delta E & = & \zeta (L,S) \{ \mathbf{L}\cdot\mathbf{S} \} \\ \ & = & \ (1/2) \zeta (L,S) \{ J(J+1)-L(L+1)-S(S+1) \} \end{matrix}

La valeur de 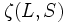\zeta (L,S)\, passe de +1 à -1 lorsque l'orbitale est plus que à moitié pleine.Ce terme donne la dépendance de l'état fondamental en énergie avec J \, .

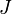Exemples

Le terme de plus faible énergie du silicium, 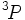{}^3\!P \, est dégénéré trois fois quand on néglige le couplage spin-orbite. Les valeurs de J lorsqu'on le prend en compte sont donc 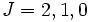J = 2,1,0 \, . Avec seulement 2 électrons dans l'orbitale (qui peut en contenir 6), elle est moins que à moitié plein, et donc le niveau d'énergie la plus basse est {}^3\!P_0 \, .

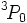Pour le soufre (S), le terme de plus faible énergie est à nouveau 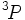{}^3\!P \, avec des valeurs de 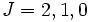J = 2,1,0 \, pour le couplage spin-orbite. Mais il y a à présent 4 électrons dans l'orbitale, le terme fondamental est donc {}^3\!P_2 \, .

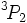États excités

Les règles de Hund marchent mieux pour la détermination de l'état fondamental d'un atome ou molécule.

Elles sont aussi assez fiables (avec échecs occasionnels) pour déterminer l'état le plus bas en énergie d'une configuration électronique excitée donnée. Alors dans l'atome d'hélium, la première règle prédit bien que l'état triplet 1s2s (3S) est plus bas que le singulet 1s2s (3S). De même pour les molécules organiques, cette règle prédit que le premier état triplet (écrit T1 dans la photochimie) est plus bas que le premier état excité singulet (S1), ce qui est généralement vrai.

Cependant les règles de Hund ne doivent pas être employées pour prévoir l'ordre des états autre que le plus bas état de chaque configuration. (Levine p.303) Par exemple, l'état fondamental de l'atome de titane possède une configuration 3d2, et l'application naïve des règles de Hund suggérerait l'ordre 3F < 3P < 1G < 1D < 1S. Mais en réalité l'état 1D est inférieure en énergie à 1G.

Références

  • P. Atkins et J. de Paula, Chimie physique (de Boeck, 3e édition française, 2008), p.341

Ces références sont celles données par la version anglaise de cet article, et n'ont pas été vérifiées.

  • Elementary Atomic Structure, physics, by G.K. Woodgate (McGraw-Hill, 1970) [ISBN 978-0-19-851156-4]
  • G.L. Miessler and D.A. Tarr, Inorganic Chemistry (Prentice-Hall, 2nd edn 1999) [ISBN 0-13-841891-8], pp.358-360
  • T. Engel and P. Reid, Physical Chemistry (Pearson Benjamin-Cummings, 2006) [ISBN 0-8053-3842-X], pp.477-479
  • I.N. Levine, Quantum Chemistry (Prentice-Hall, 4th edn 1991) [ISBN 0-205-12770-3], pp. 303-304

Voir aussi

Liens externes

Ces liens externes sont ceux donnés par la version anglaise de cet article, et n'ont pas été vérifiés.


  • Portail de la chimie Portail de la chimie
Ce document provient de « R%C3%A8gle de Hund ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Règle de multiplicité maximale de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Histoire de la chimie quantique — Histoire de la mécanique quantique Le modèle quantique d atome de 1913 de Niels Bohr, incorporant l explication de la formule de Rydberg de 1888, l hypothèse quantique de 1900 de Max Planck, i.e. que les radiations d énergies atomiques ont des… …   Wikipédia en Français

  • Histoire de la mecanique quantique — Histoire de la mécanique quantique Le modèle quantique d atome de 1913 de Niels Bohr, incorporant l explication de la formule de Rydberg de 1888, l hypothèse quantique de 1900 de Max Planck, i.e. que les radiations d énergies atomiques ont des… …   Wikipédia en Français

  • Histoire de la mécanique quantique — Le modèle quantique d atome de 1913 de Niels Bohr, incorporant l explication de la formule de Rydberg de 1888, l hypothèse quantique de 1900 de Max Planck, i.e. que les radiations d énergies atomiques ont des valeurs discrètes (ε = hν), le modèle …   Wikipédia en Français

  • LEIBNIZ (G. W.) — Dans l’histoire de la philosophie, Leibniz doit être situé à l’intersection du plus ancien et du plus moderne: traditionnel par sa filiation scolastique avouée et par le souci théologique constant dans sa pensée, il est sans nul doute le plus… …   Encyclopédie Universelle

  • Atome — Un atome (grec ancien ἄτομος [atomos], « qui ne peut être divisé »)[1] est la plus petite partie d un corps simple pouvant se combiner chimiquement avec une autre. La théorie atomiste, qui soutient l idée d une matière composée de… …   Wikipédia en Français

  • CONSCIENCE — Le mot latin conscientia est naturellement décomposé en «cum scientia». Cette étymologie suggère non seulement la connaissance de l’objet par le sujet, mais que cet objet fait toujours référence au sujet lui même. Le terme allemand Bewusstsein… …   Encyclopédie Universelle

  • ÉCOLOGIE — Le terme d’écologie (du grec oikos , demeure, et logos , science) a été proposé par E. Haeckel en 1866 pour désigner la science qui étudie les rapports entre les organismes et le milieu où ils vivent. Cette définition reste encore valable, mais… …   Encyclopédie Universelle

  • VOL (MÉCANIQUE DU) — La mécanique du vol est une application de la mécanique rationnelle à l’étude du mouvement des appareils, pilotés, autoguidés ou téléguidés n’ayant pas de contact avec le sol sur une partie de leur trajectoire. Toute action d’un pilote humain ou… …   Encyclopédie Universelle

  • ENZYMES — Tous les organismes sont le siège de certaines réactions chimiques communes connues sous le nom d’activité métabolique. Il existe de nombreuses différences de détail dans le métabolisme des divers organismes actuellement connus. Cependant, ils… …   Encyclopédie Universelle

  • RESPIRATOIRE (APPAREIL) - Pathologie — La connaissance préalable des fonctions et des mécanismes est indispensable à la compréhension des symptômes et des conséquences des maladies. Claude Bernard a en effet montré que la science clé était, pour la médecine, la physiologie, qui, seule …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”