Rugosité et adhésion

Rugosité et adhésion
Ruban adhésif

L'adhésion est l'ensemble des phénomènes physico-chimiques qui se produisent lorsque l’on met en contact intime deux matériaux, et qui ont pour effet de créer une résistance mécanique à la séparation.

Or, en général, les surfaces solides sont rugueuses ; le contact de deux surfaces est donc limité au voisinage du sommet des aspérités. Et avec un faible contact réel, l'adhésion est faible. C'est pourquoi la plupart des objets sont non collants. Par exemple, notre pouce et notre index ne collent pas ensemble par simple contact.

À l'inverse, les colles et les adhésifs ainsi que les lézards geckos, chacun à leur manière, sont suffisamment déformables pour réaliser un contact intime et permettre une bonne adhésion, malgré leur rugosité.

Sommaire

Matériaux rigides : une surface réelle de contact limitée

Histoire

Les premières mesures de rugosité sur un métal ont été effectuées par Greenwood et Williamson en 1944 à l'aide d'un appareil appelé profilomètre. Ils ont constaté que la surface pouvait être décrite comme une collection d'aspérités arrondies, de même rayon de courbure R (typiquement 100 microns pour un métal), mais de hauteur (et de largeur) variable. La hauteur typique Σ est de l'ordre de 1 micron pour un métal, et la largeur D de l'aspérité est de l'ordre de 10 microns.

Surface réelle d'interaction pour des matériaux rigides

Autour de chaque point de contact, seule une toute petite région de l'une des surfaces est très proche de l'autre surface. Pour que l'attraction de van der Waals fasse effet, il faut que la distance entre les deux surfaces reste de l'ordre d'une distance atomique (Å). Cela concerne donc une région minuscule autour de chaque contact (de rayon 0,1\,\mu{\rm m}, voir plus bas). Au total, seule une infime fraction (0,01%, voir plus bas) de la première surface est réellement en contact avec l'autre surface (ou à moins d'une distance atomique).

Estimation de la surface réelle d'interaction pour des matériaux rigides

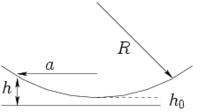
Région d'interaction entre deux surfaces

Plus précisément, l'énergie d'interaction de van der Waals par unité de surface varie comme l'inverse du carré de la distance entre les deux surfaces. Supposons donc qu'une aspérité de rayon R se situe à une distance h0 d'une surface rigide (voir figure) et corresponde à une énergie d'interaction A/h_0^2, où A est la constante de Hamacker. Alors à proximité de l'aspérité, où la distance h entre les deux surfaces est légèrement supérieure, l'énergie d'interaction vaut A / h2. L'énergie totale d'interaction entre l'aspérité et le plan s'obtient par intégration : \int_0^\infty\,\frac{A}{h^2(a)}\,2\pi\,a\,{\rm d}a, où a est la distance au point où les surfaces sont au plus près (voir figure).

Or, la distance h entre les deux surfaces s'exprime comme h\simeq h_0+a^2/(2R). Il s'ensuit que la majeure partie de l'intégrale correspond à une région où a est au maximum de l'ordre de a_{\rm rigide}\simeq\sqrt{h_0\,R}. Pour un contact à l'échelle atomique (h_0\simeq 0,1\,{\rm nm}) et pour les rayons de courbure typiques (R\simeq 100\,\mu{\rm m}), cela correspond à une région de rayon a_{\rm rigide}\simeq 0,1\,\mu{\rm m}.

Ainsi, l'essentiel de l'interaction de van der Waals est supportée par une surface de l'ordre de h_0\,R pour chaque aspérité. En moyenne, puisque les aspérités sont distantes de D, la fraction utile de la surface est de l'ordre de :

\phi\simeq\frac{a_{\rm rigide}^2}{D^2}\simeq\frac{(10^{-7})^2}{(10^{-5})^2}\simeq 0,01\%

Déformabilité et surface réelle de contact

Dans le cas où le solide rugueux est en contact avec un adhésif, ce dernier est constitué d'un matériau élastique. Sous l'effet des forces interfaciales, il se déforme localement et accroît la surface réelle de contact.

Histoire

En 1971, Johnson, Kendall et Roberts ont calculé le comportement d'adhésion directe entre une sphère et un plan élastiques. Or, les aspérités d'une surface rugueuse, même si elles ne constituent pas des sphères entières, peuvent être considérées comme des portions de sphère. C'est ce qui a suggéré à Fuller et Tabor, en 1975, de combiner le résultat de Greenwood et Williamson et celui de Johnson, Kendall et Roberts. Ils ont ainsi obtenu les conditions dans lesquelles le contact entre une surface rugueuse rigide et un plan déformable est intime.

Critère de qualité du contact

Le critère obtenu par Fuller et Tabor met en regard la rigidité du matériau, l'énergie gagnée lorsque les surfaces entrent en contact (énergie de Dupré) ainsi que les dimensions des aspérités. Il est résumé par un coefficient Q de qualité du contact, calculé plus bas.

Ce coefficient est petit (Q\ll 1, faible qualité du contact) lorsque le matériau est rigide ou que l'énergie de Dupré est faible, ou encore lorsque les aspérités sont hautes ou peu étendues. Dans ce cas, la surface de contact est réduite à un disque de faible diamètre au sommet de chaque aspérité.

À l'inverse, lorsque ce coefficient est grand (Q\gg 1), le diamètre du contact de chaque aspérité, si on le calculait de la même manière, serait supérieur à la largeur D de l'aspérité. Ainsi, en réalité, chaque aspérité est en contact total avec le matériau en vis-à-vis. Pour certaines géométries de rugosité, il est même possible que le contact soit continu d'une aspérité à ses voisines et cela peut même donner lieu au piégeage d'un peu d'air dans les creux entre aspérités au moment de la mise en contact.

En fonction des paramètres (élasticité, énergie de Dupré, dimensions), on a donc un régime de faible contact dans lequel la surface de contact peut varier, et un régime de contact complet dans lequel la surface réelle de contact est comparable à la surface nominale de contact (celle que l'on constate à l'échelle macroscopique).

Taille du contact de chaque aspérité

Chaque aspérité en contact avec le matériau déformable est comme une portion de sphère. À la mise en contact, en l'absence de force, le résultat JKR indique que le contact s'étend spontanément à une région de rayon :

a_{\rm spont}\simeq\left(\frac{R^2W}{E^\star}\right)^{1/3},

où E^\star=E/(1-\nu^2) est le module du matériau élastique (module d'Young E, renormalisé par son coefficient de Poisson ν), où W est l'énergie de Dupré, et où R est le rayon de courbure des aspérités. Cette dimension du contact peut s'exprimer en fonction de quantités plus directement accessibles par des mesures de profilométrie, à savoir la hauteur typique Σ et la largeur typique D\simeq\sqrt{\Sigma\,R} des aspérités :

a_{\rm spont}\simeq\left(\frac{D^4\,W}{\Sigma^2\,E^\star}\right)^{1/3}.

La fraction de la surface qui entre en contact spontanément dès la mise en contact s'écrit

\phi\simeq\frac{a_{\rm spont}^2}{D^2}\simeq \left(\frac{D\,W}{\Sigma^2\,E^\star}\right)^{2/3}

Pour une énergie de Dupré de 0,1 N/m, un module élastique de 105 Pa et une amplitude Σ de rugosité de l'ordre de 1 micron, le rayon de contact aspont est ainsi comparable à la largeur D des aspérités et la fraction de la surface réellement en contact est proche de 1.

Coefficient de qualité du contact

Une combinaison sans dimension de l'énergie de Dupré, du module élastique et des paramètres géométriques des aspérités, par exemple

Q=\frac{W\,D}{E^\star\,\Sigma^2},

permet d'exprimer simplement le rayon spontané de chaque contact

a_{\rm spont}\simeq Q^{1/3}\,D

ainsi que la fraction de la surface qui entre en contact spontanément dès la mise en contact :

\phi\simeq\frac{a_{\rm spont}^2}{D^2}\simeq Q^{2/3}

Les expressions ci-dessus pour le rayon aspont de contact et pour la fraction de la surface en contact intime sont valables lorsque Q\ll 1, autrement dit lorsque la qualité du contact est mauvaise. À l'inverse, lorsque Q\gg 1, une fraction non négligeable de la surface est en contact intime :

\phi\simeq 1

a_{\rm spont}\simeq D

La transition entre ces deux régimes (Q\approx 1) constitue une interprétation (Creton, Leibler, 1996) du critère de Dahlquist puisque pour des rugosités et une énergie de Dupré typiques (voir plus haut), elle correspond à un module élastique de l'ordre de 105 Pa.

Influence de la surface réelle de contact sur l'adhésion

Pour un adhésif sensible à la pression (PSA), on peut imaginer, comme Zosel, que l'énergie d'adhésion est proportionnelle à l'aire réelle de contact. On obtient alors un régime où l'énergie d'adhésion dépend par exemple du module élastique (avec une saturation lorsque le module est inférieur à une certaine valeur), ou de la pression exercée (avec une saturation lorsqu'elle est supérieure à une certaine valeur).


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Rugosité et adhésion de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Rugosité — La rugosité est une caractéristique de l’état de surface d un matériau solide. Elle est susceptible de recevoir plusieurs acceptions techniques: Sommaire 1 En géomorphologie 2 En tribologie 3 En hydraulique 4 …   Wikipédia en Français

  • Adhesion — Adhésion En physique, l adhésion est l ensemble des phénomènes physico chimiques qui se produisent lorsque l’on met en contact intime deux matériaux, dans le but de créer une résistance mécanique à la séparation. Une fois le contact établi, l… …   Wikipédia en Français

  • Adhésion religieuse — Adhésion En physique, l adhésion est l ensemble des phénomènes physico chimiques qui se produisent lorsque l’on met en contact intime deux matériaux, dans le but de créer une résistance mécanique à la séparation. Une fois le contact établi, l… …   Wikipédia en Français

  • Adhésion — En physique et en mécanique, l adhésion est l ensemble des phénomènes physico chimiques qui se produisent lorsque l’on met en contact intime deux matériaux, dans le but de créer une résistance mécanique à la séparation. Une fois le contact établi …   Wikipédia en Français

  • Adhésif — Ruban adhésif Colle liquide Un …   Wikipédia en Français

  • Adhesif — Adhésif Ruban adhésif …   Wikipédia en Français

  • Digital Surf — Création 1989 Fondateurs Christophe Mignot …   Wikipédia en Français

  • Rodage — Le rodage est une technique ancienne qui permet d ajuster parfaitement deux surfaces pour qu elles deviennent étanches, par exemple pour fermer les fioles des pharmaciens et tous les clapets des giffards des chaudières à vapeur. La technique… …   Wikipédia en Français

  • État de surface — En mécanique, l état de surface est un élément de cotation d une pièce indiquant la fonction, la rugosité, la géométrie et l aspect des surfaces usinées. Sommaire 1 Critères 1.1 Fonctions de surface 1.1.1 Surface avec fonction …   Wikipédia en Français

  • Etat de surface — État de surface En mécanique, l état de surface est un élément de cotation d une pièce indiquant la fonction, la rugosité, la géométrie et l aspect des surfaces usinées. Sommaire 1 Critères 1.1 Fonctions de surface 1.2 Défauts de surface …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”