Représentation de fresnel

Représentation de Fresnel

Pour les articles homonymes, voir Fresnel.

La représentation de Fresnel est un outil graphique permettant d'ajouter, de soustraire, de dériver et d'intégrer des fonctions sinusoïdales de même fréquence.

En physique, de nombreuses grandeurs peuvent être des fonctions sinusoïdales du temps (ou de l'espace) :

courants, tensions, puissance (électricité)
ondes :
- lumière (onde électromagnétique)
- son (onde de pression)
- chaleur (onde de température)
- élongation d'un ressort, vagues, ... (ondes mécaniques)

Pour réaliser certains calculs, on peut être conduit à réaliser un certain nombre d'opérations avec ces grandeurs sinusoïdales :

somme ou différence sont utiles en électrocinétique (loi des nœuds, loi des mailles) et pour les interférences (somme de deux ondes)
dérivation ou intégration : pour appliquer l'équation caractéristique de certains dipôles (condensateurs, inductances)

Le physicien pourra alors utiliser la représentation de Fresnel qui est un outil moins puissant mais plus visuel que les nombres complexes.

Sommaire

1 Principe
2 Cas particulier des courants et des tensions
3 Exemple d'utilisation
4 Voir aussi

Principe

À toute grandeur fonction sinusoïdale du temps d'expression :

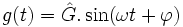$g(t) = \hat G . \sin (\omega t + \varphi )$ ,

on fait correspondre un vecteur :

$\vec G \,$

dont les caractéristiques sont les suivantes :

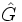Module $G \,$ = amplitude $\hat G \,$ (ou valeur efficace pour les courants et les tensions, voir remarque ci-dessous)
Angle polaire 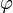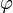$\varphi \,$ = $\varphi \,$ , phase à l'origine de la grandeur sinusoïdale

Cas particulier des courants et des tensions

Il est d'usage d'écrire ces grandeurs sous la forme :

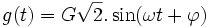$g(t) = G \sqrt{2} . \sin (\omega t + \varphi ) \,$ ,

G étant alors la valeur efficace du courant ou de la tension considérés et de choisir cette valeur pour module du vecteur de Fresnel associé. Ce n'est pas une obligation, mais le choix doit être le même pour toutes les grandeurs utilisées pour les calculs.

Exemple d'utilisation

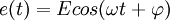Soit le circuit RC suivant soumis a une tension $e(t)=E cos(\omega t + \varphi ) \,$ :

On cherche a déterminer I

En utilisant les amplitudes et impédances complexes :

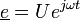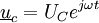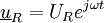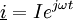
$\underline e=Ue^{j\omega t }$ , $\underline u_c=U_Ce^{j\omega t }$ , $\underline u_R=U_Re^{j\omega t }$ , $\underline i=Ie^{j\omega t }$

Loi des mailles:

$U = U C + U R = Z I$

Déterminons Z ?

$Z = Z R + Z C = R - j / (C ω)$

A partir de Z on en déduit :

I=U/Z

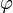$\varphi\,$ =arg(u)

En utilisant les constructions vectorielles:

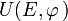$U(E,\varphi \,)$ = $U R (R I, O) + U C (I / (C ω), - π / 2)$

Soit la représentation de Fresnel:

Puis de façon simple, il suffit de faire dans cet exemple (Attention, on ne somme pas les tensions mais les amplitudes complexes) :

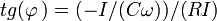
$tg(\varphi\,) = (-I/(C\omega))/(RI)$

$U 2 = ( - I / (C ω)) 2 + (R I) 2$

On peut retrouver ainsi facilement I=...

Nous avons avec la représentation de Fresnel une vision rapide de tous les signaux et la possibilité de déterminer graphiquement les résultats.

Voir aussi

Bibliographie

Liens internes

Courant alternatif

Liens externes

Portail de l’électricité et de l’électronique

Ce document provient de « Repr%C3%A9sentation de Fresnel ».

Catégorie : Théorie électrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Représentation de fresnel de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Representation de Fresnel — Représentation de Fresnel Pour les articles homonymes, voir Fresnel. La représentation de Fresnel est un outil graphique permettant d ajouter, de soustraire, de dériver et d intégrer des fonctions sinusoïdales de même fréquence. En physique, de… … Wikipédia en Français
Représentation de Fresnel — Pour les articles homonymes, voir Fresnel. La représentation de Fresnel est un outil graphique permettant d ajouter, de soustraire, de dériver et d intégrer des fonctions sinusoïdales de même fréquence. En physique, de nombreuses grandeurs… … Wikipédia en Français
Augustin Fresnel — Pour les articles homonymes, voir Fresnel. Augustin Fresnel Augustin Fresnel Naissance 10 … Wikipédia en Français
Augustin Jean Fresnel — Augustin Fresnel Pour les articles homonymes, voir Fresnel. Augustin Fresnel Augustin Jean Fresnel, né le 10 mai … Wikipédia en Français
Huygens–Fresnel principle — Wave refraction in the manner of Huygens … Wikipedia
Lentille De Fresnel — Pour les articles homonymes, voir Fresnel. La lentille de Fresnel est un type de lentille inventé par Augustin Fresnel pour équiper le système optique des phares de signalisation marine. Sa conception lui permet d obtenir une courte distance… … Wikipédia en Français
Lentille de fresnel — Pour les articles homonymes, voir Fresnel. La lentille de Fresnel est un type de lentille inventé par Augustin Fresnel pour équiper le système optique des phares de signalisation marine. Sa conception lui permet d obtenir une courte distance… … Wikipédia en Français
Lentille de Fresnel — Pour les articles homonymes, voir Fresnel. La lentille de Fresnel est un type de lentille inventé par Augustin Fresnel pour équiper le système optique des phares de signalisation marine. Sa conception lui permet d obtenir une courte distance… … Wikipédia en Français
Impedance (electricite) — Impédance (électricité) Pour les articles homonymes, voir Impédance. L impédance électrique mesure l opposition d un circuit électrique au passage d un courant alternatif sinusoïdal. La définition d impédance est une généralisation de la loi d… … Wikipédia en Français
Impédance (international) — Impédance (électricité) Pour les articles homonymes, voir Impédance. L impédance électrique mesure l opposition d un circuit électrique au passage d un courant alternatif sinusoïdal. La définition d impédance est une généralisation de la loi d… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Représentation de fresnel