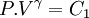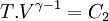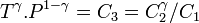Relations de laplace
- Relations de laplace
-
Loi de Laplace (thermodynamique)

Pour les articles homonymes, voir
Laplace.
En thermodynamique, lors d'une transformation thermodynamique d'un gaz parfait, plus précisément lors d'une transformation adiabatique et réversible, ou une transformation isentropique[1], la loi de Laplace est une relation qui relie la pression et le volume, la température et le volume, ou la température et la pression.
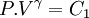
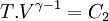
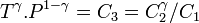
où
- P est la pression du gaz
- V est le volume occupé par le gaz
- T est la température du gaz
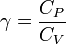 est le coefficient de Laplace du gaz parfait (sans unité), c'est-à-dire le rapport des capacités thermiques
est le coefficient de Laplace du gaz parfait (sans unité), c'est-à-dire le rapport des capacités thermiques 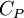 à pression constante et
à pression constante et 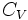 à volume constant.
à volume constant.- C1,C2 et C3 étant trois constantes différentes selon les gaz parfaits et selon les transformations thermodynamiques.
Les relations de Laplace sont valables dans le cas d'une transformation isentropique d'un gaz parfait, c'est-à-dire d'une transformation adiabatique et réversible. On suppose aussi que 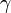 ne dépend pas de la température.
ne dépend pas de la température.
Notes
- ↑ En toute rigueur il n'existe pas d'équivalence directe entre la propriété d'isentropie et celle d'adiabacité-réversibilité. Si l'application du second principe de la thermodynamique donne de manière évidente l'implication suivante : une réaction adiabatique et réversible est isentropique, il ne permet pas de retourner cette implication. En effet, si l'isentropie d'un système est nulle, on peut seulement conclure que le terme de création est égale à l'opposé du terme d'échange. En revanche si l'on rajoute à l'hypothèse d'isentropie celle de réversibilité (ou d'adiabacité), alors on établit l'implication suivante : une réaction isentropique et adiabatique (ou réversible) est adiabatique et réversible.
 Portail de la physique
Portail de la physique
Catégories : Loi en thermodynamique | Mécanique des milieux non homogènes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Relations de laplace de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Relations de Laplace — Loi de Laplace (thermodynamique) Pour les articles homonymes, voir Laplace. En thermodynamique, lors d une transformation thermodynamique d un gaz parfait, plus précisément lors d une transformation adiabatique et réversible, ou une… … Wikipédia en Français
LAPLACE (P. S. de) — Fils d’un cultivateur, auquel l’étude fut ouverte, Laplace dut à des talents remarquables en mathématiques de s’imposer au monde savant dès les dernières années de l’Ancien Régime. Mais c’est à travers la Révolution, l’Empire et la Restauration,… … Encyclopédie Universelle
Relations de maxwell — Ne doit pas être confondu avec Équations de Maxwell. En thermodynamique, on appelle relations de Maxwell l ensemble des équations aux dérivées partielles obtenues grâce aux définitions des potentiels thermodynamiques et à l égalité de… … Wikipédia en Français
Laplace–Runge–Lenz vector — Throughout this article, vectors and their magnitudes are indicated by boldface and italic type, respectively; for example, left| mathbf{A} ight| = A. In classical mechanics, the Laplace–Runge–Lenz vector (or simply the LRL vector) is a vector… … Wikipedia
Laplace transform applied to differential equations — The use of Laplace transform makes it much easier to solve linear differential equations with given initial conditions.First consider the following relations:: mathcal{L}{f } = s mathcal{L}{f} f(0): mathcal{L}{f } = s^2 mathcal{L}{f} s f(0) f (0) … Wikipedia
Laplace's Coefficients — Harmonic Har*mon ic (h[aum]r*m[o^]n [i^]k), Harmonical Har*mon ic*al ( [i^]*kal), a. [L. harmonicus, Gr. armoniko s; cf. F. harmonique. See {Harmony}.] 1. Concordant; musical; consonant; as, harmonic sounds. [1913 Webster] Harmonic twang! of… … The Collaborative International Dictionary of English
Relations de Maxwell — Ne doit pas être confondu avec Équations de Maxwell. En thermodynamique, on appelle relations de Maxwell l ensemble des équations aux dérivées partielles obtenues grâce aux définitions des potentiels thermodynamiques et à l égalité de… … Wikipédia en Français
Loi de Laplace (thermodynamique) — Pour les articles homonymes, voir Laplace. En thermodynamique, lors d une transformation isentropique d un gaz parfait, par exemple lors d une transformation adiabatique et réversible[1], la loi de Laplace est une relation qui relie la pression… … Wikipédia en Français
Vecteur de Laplace-Runge-Lenz — Vecteur de Runge Lenz Dans cet article les vecteurs et leurs normes sont indiqués respectivement en gras et italique. Par exemple : . En mécanique classique, le vecteur de Runge Lenz ou invariant de Runge Lenz est un vecteur utilisé… … Wikipédia en Français
Pierre-Simon Laplace — Pour les articles homonymes, voir Laplace. Pierre Simon Laplace … Wikipédia en Français
 Pour les articles homonymes, voir Laplace.
Pour les articles homonymes, voir Laplace.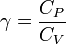 est le coefficient de Laplace du gaz parfait (sans unité), c'est-à-dire le rapport des capacités thermiques
est le coefficient de Laplace du gaz parfait (sans unité), c'est-à-dire le rapport des capacités thermiques 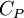 à pression constante et
à pression constante et 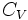 à volume constant.
à volume constant.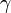 ne dépend pas de la température.
ne dépend pas de la température.