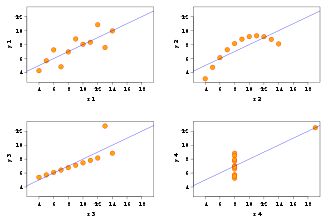
- Quartet d'Anscombe
-
Les quatre ensembles de données possèdent les mêmes propriétés statistiques simples, mais leur expression graphique est très différente.
Le quartet d'Anscombe comprend quatre ensemble de données qui possèdent les mêmes propriétés statistiques simples, mais qui sont très différents lorsqu'ils sont comparés à l'aide de graphiques. Ils ont été construits en 1973 par le statisticien Francis Anscombe dans le but de démontrer l'importance de tracer des graphiques avant d'analyser un ensemble de données, car ce tracé permet d'estimer l'incidence des données aberrantes sur les propriétés statistiques de l'ensemble de données.
Sommaire
Présentation
Chaque ensemble de données contient 11 points. Les quatre ensembles présentent ces propriétés :
Propriété Valeur Moyenne des x 9.0 Variance des x 10.0 Moyenne des y 7.5 Variance des y 3.75 Corrélation entre les x et les y 0.816 Équation de la droite de régression linéaire y = 3 + 0,5x Somme des carrés des erreurs
relativement à la moyenne110,0 Le premier ensemble (en haut à gauche) semble être distribué au hasard, ce qui permet d'inférer que les variables ont une certaine corrélation. Le deuxième (en haut à droite) n'est pas distribué au hasard. Il existe une relation non linéaire, fortement correlée, entre les deux variables : pour cette raison, les coefficients de corrélation de Pearson sont inutiles. Dans le troisième ensemble (en bas à gauche), la corrélation linéaire est parfaite sauf pour une donnée aberrante qui influe sur le coefficient de corrélation, le faisant passer de 1 (pour les 10 premières données) à 0.81 (pour les 11 données). Finalement, le quatrième ensemble (en bas à droite) démontre qu'une seule donnée aberrante suffit pour obtenir un coefficient de corrélation élevé, même si les deux variables ne sont pas linéairement corrélées.
Dans la première page du premier chapitre de son ouvrage, The Visual Display of Quantitative Information, Edward Tufte utilise le quartet pour démontrer l'importance du graphique avant d'analyser l'ensemble de données.
Les ensembles de données sont comme suit (les valeurs des x sont les mêmes pour les trois premiers ensembles.)
Quartet d'Ascombe I II III IV x y x y x y x y 10.0 8.04 10.0 9.14 10.0 7.46 8.0 6.58 8.0 6.95 8.0 8.14 8.0 6.77 8.0 5.76 13.0 7.58 13.0 8.74 13.0 12.74 8.0 7.71 9.0 8.81 9.0 8.77 9.0 7.11 8.0 8.84 11.0 8.33 11.0 9.26 11.0 7.81 8.0 8.47 14.0 9.96 14.0 8.10 14.0 8.84 8.0 7.04 6.0 7.24 6.0 6.13 6.0 6.08 8.0 5.25 4.0 4.26 4.0 3.10 4.0 5.39 19.0 12.50 12.0 10.84 12.0 9.13 12.0 8.15 8.0 5.56 7.0 4.82 7.0 7.26 7.0 6.42 8.0 7.91 5.0 5.68 5.0 4.74 5.0 5.73 8.0 6.89 Une procédure pour créer d'autres ensembles de données exhibant les mêmes propriétés statistiques simples, mais des représentations graphiques dissemblables sont proposées dans les ouvrages de la bibliographie.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Anscombe's quartet » (voir la liste des auteurs)
Voir aussi
Liens externes
- (en) « Visualisation and Transformation of Data », Department of Physics, Université de Toronto
- (en) « Curve fitting », Central Queensland University, Australie
Bibliographie
- F.J. Anscombe, « Graphs in Statistical Analysis », American Statistician, 27 (February 1973), 17-21.
- Edward Tufte (2001). The Visual Display of Quantitative Information, 2nd Edition, Cheshire, CT: Graphics Press. ISBN 0961392142
- Sangit Chatterjee et Aykut Firat (2007), « Generating Data with Identical Statistics but Dissimilar Graphics: A Follow up to the Anscombe Dataset », American Statistician, 61(3), 248-254. doi:10.1198/000313007X220057
Portail des probabilités et des statistiques
Wikimedia Foundation. 2010.
