Quadripôle

Quadripôle
Un quadripôle

Un quadripôle, ou quadrupôle, est un composant ou un circuit (ensemble de composants) à deux entrées et deux sorties, permettant le transfert d'énergie entre deux dipôles.

Les signaux électriques en entrée et en sortie peuvent être de nature différente (tension, courant, puissance). On doit les premières études sur les quadripôles au mathématicien allemand Franz Breisig dans les années 1920.

On distingue 3 types de quadripôles :

  • les quadripôles actifs
  • les quadripôles passifs
  • les quadripôles linéaires

Sommaire

Symbolisation

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Fonction de transfert

Définition de la fonction de transfert T d’un quadripôle linéaire en régime alternatif sinusoïdal :

– C'est un nombre complexe T= T (j*ώ) T dépend de la fréquence et de la charge placée en sortie.

– |T|=T= Rapport entre les valeurs efficaces du signal de sortie et du signal d'entrée.

– Arg (T) = différence de phase du signal de sortie par rapport au signal d'entrée.

Coefficients d'amplification

Ce sont des fonctions de transfert particulières.

  • Coefficient d'amplification en tension : T=Av= US/Ue
  • Coefficient d'amplification en courant : T=Ai= IS/Ie

On définit aussi le coefficient d'amplification en puissance:

Ap= US*IS*cos(φS)/Ue*Ie*cos(φe) [bien que ce ne soit pas un rapport de nombres complexes associés à des signaux].

⇒ Avec (φS) le déphasage de uS par rapport à iS et (φe) le déphasage de ue par rapport à ie.

Ces coefficients dépendent en général de la fréquence et de la charge en sortie.

Gains

Comme les modules de ces coefficients peuvent varier de façon importante lorsque la fréquence varie, on utilise une autre grandeur qui "tasse" ces variations.

  • Gain en tension : Gv=20Log (Us/Ue)
  • Gain en courant : Gi=20Log (Is/Ie)
  • Gain en puissance : Gp=10log (Ps/Pe).

Les gains s'expriment en dB.

  • Lorsque T est multiplié par 10, G=20logT augmente de 20 dB ;
  • Le gain devient négatif si T<1.
  • Lorsque Av double, Gv augmente de 6dB.

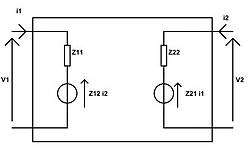
Relations en impédances

Quadripôle Z

On exprime les tensions en fonction des courants :

{V_1 \choose V_2} = \begin{pmatrix} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{pmatrix}{I_1 \choose I_2} .

Avec :

Z_{11} = {V_1 \over I_1 } \bigg|_{I_2 = 0} \qquad Z_{12} = {V_1 \over I_2 } \bigg|_{I_1 = 0}
Z_{21} = {V_2 \over I_1 } \bigg|_{I_2 = 0} \qquad Z_{22} = {V_2 \over I_2 } \bigg|_{I_1 = 0}


On appelle Z11 l'impédance d'entrée du quadripôle ; Z12 l'impédance de transfert inverse du quadripôle ; Z21 l'impédance de transfert du quadripôle ; Z22 l'impédance de sortie du quadripôle.

Relations en admittances

Quadripôle Y

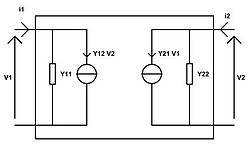
On exprime les courants en fonction des tensions :

{I_1 \choose I_2} = \begin{pmatrix} Y_{11} & Y_{12} \\ Y_{21} & Y_{22} \end{pmatrix}{V_1 \choose V_2} .

Avec :

Y_{11} = {I_1 \over V_1 } \bigg|_{V_2 = 0} \qquad Y_{12} = {I_1 \over V_2 } \bigg|_{V_1 = 0}
Y_{21} = {I_2 \over V_1 } \bigg|_{V_2 = 0} \qquad Y_{22} = {I_2 \over V_2 } \bigg|_{V_1 = 0}


On appelle Y11 l'admittance d'entrée du quadripôle ; Y12 l'admittance de transfert inverse du quadripôle ; Y21 l'admittance de transfert du quadripôle ; Y22 l'admittance de sortie du quadripôle.

Relations hybrides

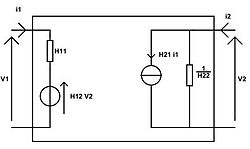
Article détaillé : Paramètre hybride.
Quadripôle H

Ces relations sont utiles lors de l'étude des transistors.

{V_1 \choose I_2} = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{pmatrix}{I_1 \choose V_2} .

Avec :

h_{11} = {V_1 \over I_1 } \bigg|_{V_2 = 0} \qquad h_{12} = {V_1 \over V_2 } \bigg|_{I_1 = 0}
h_{21} = {I_2 \over I_1 } \bigg|_{V_2 = 0} \qquad h_{22} = {I_2 \over V_2 } \bigg|_{I_1 = 0}


On peut noter que H11 = Z11 et que H22 = Y22.

On appelle H11 l'impédance d'entrée du quadripôle ; H12 le gain inverse en tension du quadripôle ; H21 le gain en courant de transfert du quadripôle ; H22 l'admittance de sortie du quadripôle.

Le calcul matriciel s'adapte très bien aux quadripôles et permet d'obtenir les fonctions de transferts des circuits électroniques quand d'autres méthodes s'égarent dans un formalisme abscons, source d'erreurs et de pertes de temps.

Le courant de sortie du premier quadripôle étant l'opposé du courant d'entrée du quadripôle suivant, on utilise plutôt le système d'équations linéaires suivant :

V1 = a11.V2 + a12.( − I2)

I1 = a21.V2 + a22.( − I2)

Les coefficients aij forment les éléments de la matrice carrée "chaine directe" (abrégée MCD). L'analyse d'un filtre passif ou actif peut être simplifiée par décomposition en quadripôles élémentaires (Z série) et (Y parallèle) représenté chacun par une matrice "chaine directe". Les termes A11 et A12 de la matrice résultante servent à définir respectivement la fonction de transfert v2/v1(pour i2=0) ainsi que l'impédance d'entrée v1/i1 (pour i2=0).

Ainsi, la MCD d'une impédance série Z présentée sous forme d'un quadripôle sera {1 Z;0 1}; celle d'une admittance parallèle sera {1 0;Y 1}...

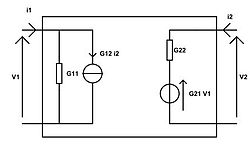
Relations hybrides inverse

Quadripôle G

Les relations hybrides inverse sont très peu utilisées, mais elles existent.









Théorème de réciprocité dans les quadripôles passifs

On a les relations : Y12 = Y21, Z12 = Z21, H12 = -H21 et ΔT = 1.


Quadripôle symétrique

Les deux accès d'un quadripôle symétrique sont indiscernables: les indices correspondant, 1 et 2, des paramètres de matrices impédance ou admittance sont donc permutables sans changement. En conséquence, pour les quadripôles symétriques, en plus de posséder les propriétés de réciprocité, on a les relations Y11 = Y22 et Z11 = Z22.

Association de deux quadripôles

Désignation Schéma Propriétés
série [Z] = [Z1]+ [Z'1]
parallèle [Y] = [Y1]+ [Y'1]
parallèle-série [G] = [G1] + [G'1]
série-parallèle [H] = [H1] + [H'1]
cascade [T] = [T1] [T'1]

Conversion des matrices

matrice de transfert matrice impédance matrice admittance matrice hybride
T Z Y H
T 
 ⌈T11      T12⌉
 ⌊T21      T22⌋

 ⌈Z11/Z21     -ΔZ/Z21⌉
 ⌊1/Z21      -Z22/Z21⌋

 ⌈-Y22/Y21      1/Y21⌉
 ⌊-ΔY/Y21     Y11/Y21⌋

 ⌈-ΔH/H21    -H11/H21⌉
 ⌊-H22/H21     -1/H21⌋
Z 
 ⌈T11/T21      ΔT/T21⌉
 ⌊1/T21       T22/T21⌋

 ⌈Z11             Z12⌉
 ⌊Z21             Z22⌋

 ⌈Y22/ΔY      -Y12/ΔY⌉
 ⌊-Y21/ΔY      Y11/ΔY⌋

 ⌈ΔH/H22      H12/H22⌉
 ⌊-H21/H22      1/H22⌋
Y 
 ⌈T22/T12     -ΔT/T12⌉
 ⌊-1/T12      T11/T12⌋

 ⌈Z22/ΔZ      -Z12/ΔZ⌉
 ⌊-Z21/ΔZ      Z11/ΔZ⌋

 ⌈Y11             Y12⌉
 ⌊Y21             Y22⌋

 ⌈1/H11      -H12/H11⌉
 ⌊H21/H11      ΔH/H11⌋
H 
 ⌈T12/T22      ΔT/T22⌉
 ⌊-1/T22      T21/T22⌋

 ⌈ΔZ/Z22      Z12/Z22⌉
 ⌊-Z21/Z22      1/Z22⌋

 ⌈1/Y11      -Y12/Y11⌉
 ⌊Y21/Y11      ΔY/Y11⌋

 ⌈H11             H12⌉
 ⌊H21             H22⌋

Liens externes

Voir aussi

  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Quadripôle de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Quadripole — Quadripôle Un quadripôle Un quadripôle, ou quadrupôle, est un composant ou un circuit (ensemble de composants) à deux entrées et deux sorties, permettant le transfert d énergie entre deux dipôles. Les signaux électriques en entrée et en sortie… …   Wikipédia en Français

  • quadripôle — [ k(w)adripol ] n. m. • 1926; de quadri et pôle ♦ Électron. Circuit électrique possédant quatre bornes, une paire de bornes constituant l entrée, l autre la sortie. Un quadripôle amplificateur. ● quadripôle nom masculin Réseau électrique à deux… …   Encyclopédie Universelle

  • quadripole — keturpolis statusas T sritis automatika atitikmenys: angl. four pole; four terminal network; quadripole; two port; two port network vok. Vierpol, m rus. четырёхполюсник, m pranc. quadripôle, m; tétrapôle, m …   Automatikos terminų žodynas

  • quadripôle — keturpolis statusas T sritis automatika atitikmenys: angl. four pole; four terminal network; quadripole; two port; two port network vok. Vierpol, m rus. четырёхполюсник, m pranc. quadripôle, m; tétrapôle, m …   Automatikos terminų žodynas

  • quadripole — keturpolis statusas T sritis fizika atitikmenys: angl. four terminal network; quadripole vok. Vierpol, m rus. четырёхполюсник, m pranc. quadripôle, m; réseau à quatre bornes, m …   Fizikos terminų žodynas

  • quadripôle — keturpolis statusas T sritis fizika atitikmenys: angl. four terminal network; quadripole vok. Vierpol, m rus. четырёхполюсник, m pranc. quadripôle, m; réseau à quatre bornes, m …   Fizikos terminų žodynas

  • quadripôle en T — T keturpolis statusas T sritis radioelektronika atitikmenys: angl. T section four terminal network; T section two port vok. T Glied, n; T Vierpol, m rus. Т образный четырёхполюсник, m pranc. quadripôle en T, m …   Radioelektronikos terminų žodynas

  • quadripôle — kvadrupolis statusas T sritis fizika atitikmenys: angl. quadrupole vok. Quadrupol, m rus. квадруполь, m pranc. quadripôle, m; quadrupôle, m …   Fizikos terminų žodynas

  • quadripole system — keturpolė sistema statusas T sritis automatika atitikmenys: angl. fourpole system; quadripole system vok. Vierpolsystem, n rus. четырёхполюсная система, f pranc. système de quadripôle, m …   Automatikos terminų žodynas

  • quadripôle actif — aktyvusis keturpolis statusas T sritis automatika atitikmenys: angl. active four terminal network; active quadripole vok. aktiver Vierpol, m rus. активный четырёхполюсник, m pranc. quadripôle actif, m …   Automatikos terminų žodynas

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”