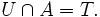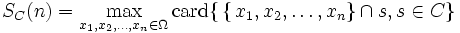Pulverisation

Le terme de pulvérisation a été introduit en 1975 par J. M. Steele dans sa thèse de doctorat, à l'université de Stanford.

Le concept de pulvérisation d'un ensemble de points joue un rôle important dans la théorie de Vapnik-Chervonenkis, également connue sous le nom de théorie VC. La pulvérisation et la théorie VC sont utilisées dans l'étude des processus empiriques ainsi qu'en théorie de l'apprentissage automatique statistique.

Sommaire 1 Définition 2 Coefficient de pulvérisation 3 classe de Vapnik-Chervonenkis 4 Sources

Définition

Soient C une classe d'ensembles et A un ensemble. On dit que C pulvérise A si et seulement si, pour tout sous-ensemble T de A, il existe un élément U appartenant à C tel que

Ceci équivaut encore à dire que C pulvérise A si et seulement si l'ensemble des parties de l'ensemble A, P(A), est égal à l'ensemble { U ∩ A | U ∈ C }.

Par exemple, la classe C des disques du plan (lorsqu'on se place dans un espace à deux dimensions) ne peut pas pulvériser tous les ensembles F de quatre points, alors qu'en revanche la classe des ensembles convexes du plan pulvérise tout ensemble fini du cercle unité.

Coefficient de pulvérisation

Pour mesurer la richesse d'une collection C d'ensembles, on utilise le concept de coefficients de pulvérisation (également appelés fonction de croissance). Pour une collection C d'ensembles 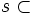Ω, où Ω est un ensemble, on définit le n^ième coefficient de pulvérisation de C par

où "card" signifie cardinal, c'est-à-dire, le nombre d'éléments d'un ensemble.

De cette définition découlent les propriétés suivantes :

1. 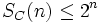pour tout n.

2. S_C(n) = 2ⁿ, si et seulement s'il existe un ensemble de cardinal n pulvérisé par C.

3. S'il existe N > 1 tel que S_C(N) < 2^N, alors S_C(n) < 2ⁿ pour tout 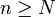(en d'autres termes, une classe d'ensembles qui ne peut pulvériser aucun ensemble à N éléments ne pourra pas non plus pulvériser d'ensemble plus grand).

classe de Vapnik-Chervonenkis

La dimension VC d'une classe C est définie par

VC(C) = min_n{n:S_C(n) < 2ⁿ} ou, de manière alternative, par : VC₀(C) = max_n{n:S_C(n) = 2ⁿ}

On remarquera qu'on a : VC(C) = VC₀(C) + 1.

On dira que la dimension VC d'une classe est infinie si pour tout n il existe un ensemble à n éléments pulvérisé par C (on a alors, pour tout entier naturel n, S_C(n) = 2ⁿ).

Les classes de dimension VC finie sont appelées classes de Vapnik-Chervonenkis ou classes VC. Une classe d'ensembles est une classe uniformément Glivenko-Cantelli si et seulement si c'est une classe VC.

Sources

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Shattering ».

• [pdf] Cours sur la theorie de l’apprentissage statistique (selon V. Vapnik) de François Denis, de l'Équipe Bases de Données et Apprentissage du Laboratoire d’Informatique Fondamentale de Marseille
• (en) cours sur la dimension VC de Andrew Moore
• (en) V. Vapnik et A. Chervonenkis. "On the uniform convergence of relative frequencies of events to their probabilities." (De la convergence uniforme des fréquences relatives des événements vers leur probabilité) Theory of Probability and its Applications (Théorie de la probabilité et ses applications), 16(2):264--280, 1971.
• (en) A. Blumer, A. Ehrenfeucht, D. Haussler, et M. K. Warmuth. "Learnability and the Vapnik-Chervonenkis dimension." (Capacité d'apprentissage et dimension de Vapnik-Chervonenkis) Journal of the ACM, 36(4):929--865, 1989.
• (en) Wencour, R.S., R.M. Dudley (1981), "Some special Vapnik-Chervonenkis classes"(Classes spéciales de Vapnik-Chervonenkis), Discrete Math, 33, 1981, 313-318.
• (en) Steele, J.M. (1975), "Combinatorial Entropy and Uniform Limit Laws"(Entropie Combinatoire et lois de convergence uniforme), thèse de doctorat de mathématiques de l'université de Stanford.
• (en) Steele, J.M. (1978), "Empirical discrepancies and subadditive processes"(Divergences empiriques et processus sous-additifs), Annals of Probability, 6, 118--227.

• Portail des mathématiques
• Portail de l’informatique