- Puissance musculaire humaine et bicyclette
-
L’évaluation des consommations d’énergie lors de randonnées cyclistes remonte, en France, aux années 1980 et suivantes et a été faite
- par des universitaires qui ont publié leurs travaux dans des journaux scientifiques
- par des amateurs cyclotouristes qui ont publié ou non des ouvrages pratiques
- par des professionnels du vélo de course – qui avec et grâce à leurs sponsors - ont étudié ces paramètres en vue d’améliorer les performances du sportif cycliste et/ou de sa machine : ces études relèvent quasiment du secret industriel, ce qui fait que peu de ces études sont rendues publiques.
Sommaire
Mesure de la puissance musculaire humaine
Cette mesure se fait généralement sur des machines statiques singeant la bicyclette et sur lesquelles la force musculaire met en mouvement une roue magnétique plus ou moins freinée par un aimant. Cette roue est en effet située dans l’entrefer d’un aimant qui peut être plus ou moins rapproché de la roue ce qui entraîne une résistance variable au pédalage. On calcule ou on mesure la puissance développée en fonction des conditions d’aimantation et de la fréquence de pédalage. Les constructeurs de ces appareils les dotent d’un cadran renseignant différents paramètres : vitesse de pédalage, puissance développée en watts, « kilomètres parcourus », calories consommées et plus récemment pour les appareils grand public les fréquences des pulsations cardiaques. Dans un premier temps ces appareils étaient essentiellement médicaux (pratique des tests d’effort en cardiologie) mais l’engouement pour un exercice physique plus fréquent a permis la diffusion d’appareils de plus en plus sophistiqués vers le grand public. Les mesures des puissances obtenues sur ces appareils, même quand ils sont de qualité, ne représentent pas vraiment l’effort réel lors d’une randonnée en vélo en extérieur : l’absence de ventilation qui conduit à une sudation excessive en est l’importante différence. Il est malgré tout utile de comparer les résultats obtenus sur ces machines à ceux auxquels les calculs suivants vont conduire.
Puissance musculaire nécessaire à la pratique du cyclisme
Travaux de JP Mariot
Ils datent d’avril 1984 et ont été publiés dans la revue de Physique Appliquée 19 (1984) pp 349-357. Ils montrent que la puissance que le cycliste doit fournir pour mouvoir sa machine sur une route plate peut se décomposer en deux termes.
1er Terme : Si V est la vitesse en mètre par seconde, ρ la masse volumique de l’air en kg/m3, S.Cx un facteur combiné entre S la surface frontale (cycliste plus sa machine) frappée par l’air et Cx le facteur qui représente la facilité avec laquelle le mobile « cycliste+machine» pénètre dans l’air (on parle d’aérodynamisme),
la puissance consommée par la résistance de l’air régit le premier terme selon l’expression suivante

Pour un amateur cycliste, cette expression peut s’écrire plus simplement en remplaçant les paramètres par leurs valeurs probables

En effet ρ à 21 °C et à 1 bar est égal à 1,205 kg.m-3 et S.Cx pour la plupart des amateurs qui circulent les mains en haut du guidon et le torse frappant l’air est au moins de 0,43 m²
Dans le cas d'un vélo couché non caréné, S et Cx sont plus faibles et cette puissance devient:
Si l'on ajoute une pointe arrière aérodynamique à ce vélo couché, la trainée diminue encore :

2e Terme : Les frottements mécaniques (organes de transmission du vélo et frottements des pneus sur la route) représentent le second terme et on peut écrire :
Pour les amateurs cyclistes disposant de vélos moyenne gamme, la combinaison de g et K conduit à une valeur de 0,1 et l’équation se simplifie en :

Où m représente le poids total du cycliste et de sa machine en kg et V sa vitesse en m.s-1
L'équation générale permettant le calcul de la puissance nécessaire pour rouler sur une route plate (P (sur plat) sera donc la suivante


L'équation pour un cycliste amateur s'écrira donc


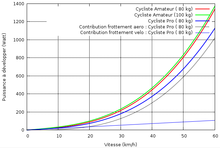
On voit que le deuxième terme est d’ordre 1 par rapport à la vitesse de déplacement contrairement au premier terme qui est d’ordre 3 par rapport à cette vitesse : plus on roule vite sur une route plate et plus la résistance de l’air prend relativement d’importance vis-à-vis des frottements mécaniques. Les paramètres évalués pour les amateurs sont nettement plus faibles pour les coureurs professionnels qui se positionnent de façon plus aérodynamique (S.Cx descendant à 0,36 m²) et dont les machines ont un rendement bien meilleur et des pneus étudiés qui les amènent à un facteur 0,08 voire moins dans la puissance dépensée par frottement. L’évolution des profils des vélos professionnels permet encore d’améliorer la pénétration dans l’air. Ainsi, avec un vélo couché non caréné et des roues de grands diamètre de bon rendement la puissance devient :


Études de Jacques Roux : « Guide du vélo en montagne » (éditions ALTIGRAPH BP1 49080 Bouchemaine)
Ces réflexions d’un amateur cyclotouriste sont fondées sur les travaux cités précédemment : il les a utilisés pour prévoir la capacité d’ascension de cols variés et connaître les durées approximatives de ces ascensions ainsi que les braquets à prévoir pour ne pas mettre pied à terre durant l’ascension.
La démarche l’a conduit à proposer des abaques et des tableaux pour éviter les calculs par itérations qu’impliquent les équations définies dans le paragraphe précédent. Il a même proposé, durant les années 1990 ces évaluations sur le Minitel français (3615 Totem).
Les travaux de JP Mariot avaient également abordé l’influence de la gravité mais Jacques Roux a développé une approche pratique compte tenu que l’ascension de grands cols – dont les pentes tournent autour de 8 à 10% voire plus – implique des vitesses d’ascension faibles qui minimisent les deux termes de calculs des puissances consommées pour résister à l’air et s’opposer aux frottements.
La puissance qu’il faut développer pour s’élever est fonction du poids, de la pente (p en %) et de la vitesse d’ascension. Le travail effectué (W) lors de l’ascension de h mètres (dénivelé) sera :

La puissance « ascensionnelle » sera
 et comme h = déplacement linéaire *p (%) on pourra écrire :
et comme h = déplacement linéaire *p (%) on pourra écrire :
Plus précisément:


L'approximation
 surestime de moins de 1% Pasc tant que la pente est inférieure à 14%. Avec 10% de pente, l'approximation surestime Pasc de 0,5%.
surestime de moins de 1% Pasc tant que la pente est inférieure à 14%. Avec 10% de pente, l'approximation surestime Pasc de 0,5%.L’auteur part de la mesure de la puissance du cycliste sur un parcours le plus plat possible et relativement long. En fait il distingue implicitement une « puissance efficace moyenne » de la puissance que l’on pourrait par exemple mesurer lors d’un test d’effort où après quelques minutes on atteint la fréquence cardiaque maximale théorique et donc la puissance maximale. Cette puissance maximale n’est disponible pour l’individu qu’en de courts instants. Il est hors de question de tabler sur une telle puissance maximale pour grimper un col durant une à plusieurs heures. C’est la raison pour laquelle le parcours de plat testé doit comporter suffisamment de kilomètres d’une part pour conduire à des chiffres assez précis et d’autre part pour être représentatif d’un effort équivalent en montagne. Je crois avoir observé que « puissance efficace moyenne » est à peine les deux tiers de la puissance maximale. Cela s’améliore avec l’entraînement et avec la condition physique.
Exemple : Si la vitesse moyenne mesurée sur plat est de 27 km/h soit 7,5 m/s, la puissance développée sur plat selon les travaux de Mariot est de :

 .
.Cette puissance pourra servir durant l’ascension d’un col dont la pente moyenne est de 8 % et conduira à une vitesse V exprimée en m/s en négligeant les facteurs de résistance de l’air et des frottements puisque la vitesse sera faible :

D’où V = 2,6 m/s soit 9,3 km/h. Si la longueur du col est de 10 km il faudra prévoir 1 heure et 5 minutes pour le gravir.
Cette valeur est par excès car les forces de résistance à l'air et aux frottements n'ont pas été intégrées au calcul : si on veut en tenir compte, il faudra résoudre l'équation du 3e degré ci-dessous qu'on ne peut résoudre que par itérations ou grâce aux tableaux établis par Jacques Roux. La différence n'est quand même pas négligeable.



Avec un vélo couché non caréné qui a des roues d'un bon rendement, cette puissance devient:


En ce qui concerne l'application de ces notions aux calculs pratiques on se reportera à l'évaluation de la puissance exercée en vélo.Évaluations des dépenses caloriques
Si on dispose d'un cardio-fréquencemètre avec les fonctions de bornage de la fréquence cardiaque (avertissement par bip si on sort de l'intervalle choisi) et que le temps passé dans cet intervalle est comptabilisé on peut évaluer la dépense calorique durant une randonnée par la méthode décrite ci-dessous.
Relation entre puissance et consommation calorique:
Le travail et la quantité de chaleur sont reliés par la relation de Joule : W = J * Q ( W étant le travail, Q la quantité de chaleur et J = 4,18)
La puissance et le travail sont reliés par la relation P = W / t (P étant la puissance, W le travail et t le temps)
On peut donc écrire que P = ( J * Q )/t soit P en watts = ( 4,18* Q )/(3600) Q étant exprimée en "petite calorie"
On peut écrire Q en kilocalories = ( 3600 * P ) /(4,18*1000) soit Q KCal = 0,86 * P en watts
Cette relation n'est valable que pour un rendement de 100%.
En fait le rendement de la "machine humaine" se situe plutôt entre 20 et 25% et dépend des capacités intrinsèques de l'individu et de son entraînement.
On peut écrire , si le rendement est de 20% Q Kcal = 4,3 P en watts
Si le rendement est de 25% (champions en bonnes conditions) Q Kcal = 3,5 P en watts
Pour les cyclistes amateurs sur lesquels l'article a été orienté on dira que son rendement est de l'ordre de 22 à 23 % Q en Kcal = 4 * P en watts
Cela signifie que le cycliste qui a été retenu ci-dessus et qui peut développer une puissance de 173 watts aura une consommation calorique voisine de:
173 * 4 soit 692 Kcal par heure (ou 2900 kilojoules par heure si on observe la réglementation actuelle des unités)
Puissance développée sur plat dans une zone précise de fréquence cardiaque :
L'épreuve de mesure de la vitesse moyenne sur plat, effectuée dans des conditions proches de celles que l'on trouvera dans l'ascension d'un col implique plutôt d'être au maximum de sa puissance moyenne effective. On peut très bien faire cette épreuve sur plat en se calant dans une zone de fréquence cardiaque donnée et bien en dessous de sa fréquence élevée supportable : la vitesse moyenne sera alors évidemment moindre. On pourra alors dire qu'entre les deux fréquences choisies on développe la puissance calculée à partir de la vitesse observée.
En étudiant précisément plusieurs intervalles on pourra établir une relation entre zone de fréquence cardiaque et puissance développée pour un individu donné.
Consommation calorique lors d'un circuit fermé:
Si on s'impose de faire cette randonnée dans une zone de fréquence cardiaque choisie (FCC) , on pourra calculer la dépense calorique en partant du temps comptabilisé dans la zone FCC et de la puissance développée à cette FCC.
Sources
« La puissance musculaire humaine en vélo », de Jacques Antoniewski, sur son site personnel (page fournissant une documentation complémentaire sur les calculs de puissance musculaire), et reproduit ici avec son agrément.
Catégories :- Bicyclette
- Cyclisme
- Physiologie du système cardio-vasculaire
- Muscle
Wikimedia Foundation. 2010.