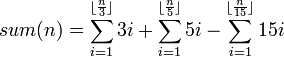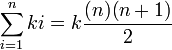- Project euler
-
Project Euler

Project EulerURL projecteuler.net Commercial non Type de site résolution de problèmes Langue(s) anglais Inscription gratuite Créé par Colin Hughes (aka Euler) Lancement 5 octobre, 2001 État actuel en activité modifier 
Project Euler est un site web dédié à une série de problèmes mathématiques dans l'intention d'être résolus grâce à des programmes informatiques. Le but du projet est d'attirer des adultes et des élèves intéressés par les mathématiques et l'informatique. Cela consiste actuellement en plus de 250 problèmes de difficulté variable ; chaque problème est conçu pour exécuter en moins d'une minute un algorithme efficace sur un ordinateur à puissance modeste. De nouvelles questions ont été progressivement ajoutées depuis la création du projet en 2001. Le site présente un forum spécifique à chaque problème, accessible après que l'utilisateur ait résolu le problème en question. Il y a également une section "Scores" qui classe les utilisateurs selon le nombre de problèmes résolus. Il existe 5 différents niveaux de classement (dénotés par les solides de Platon), plus un niveau représenté par une boule, plus un niveau spécial qui range les membres qui ont résolus au moins la moitié des 25 problèmes les plus récents.
Exemple de problème et solutions
La traduction du premier problème pourrait être :
Si on liste tous les nombres naturels inférieurs à 10 qui sont multiples de 3 ou 5, on obtient 3, 5, 6 et 9. La somme de ces nombres est 23. Trouvez la somme de tous les multiples de 3 ou de 5 inférieurs à 1000.
Bien que ce problème soit plus simple que le problème typique, il sert à illustrer la différence potentielle qu'effectue un algorithme efficace. L'algorithme brute-force examine chaque entier naturel plus petit que 1000 et garde une somme courante de ces critères rencontrés. Cette méthode est simple à implémenter, comme le montrent les exemples suivants dans différents langages de programmation :
PHP:
<?php $sum = 0; for ($i = 0; $i < 1000; $i++) if ( $i % 3 == 0 || $i % 5 == 0 ) $sum += $i; echo $sum; ?>
print sum(x for x in xrange(1, 1000) if x%3==0 or x%5 == 0)
C++:
#include <iostream> using namespace std; int main( ) { int sum = 0; for (int i = 0; i < 1000; i++) if ( i % 3 == 0 || i % 5 == 0 ) sum += i; cout << sum << endl; return 0; }
Java:
public class Main { public static void main(String[] args) { int sum = 0; for (int i = 0; i < 1000; i++) if ( i % 3 == 0 || i % 5 == 0 ) sum += i; System.out.println(sum); } }
var sum = 0; for(var i = 1; i < 1000; i++) { if(i % 3 || i % 5) sum += i; } alert(sum);
Pour les problèmes plus complexes, l'importance de trouver un algorithme efficace s'accroît. Pour ce problème, nous pouvons réduire 1000 opérations par une poignée en utilisant le principe d'inclusion-exclusion et une forme fine de la formule de somme :
Implémentation en Python:
def sum1toN(n): return n * (n + 1) / 2 def sumMultiples(limit, a): return sum1toN((limit - 1) / a) * a sumMultiples(1000, 3) + sumMultiples(1000, 5) - sumMultiples(1000, 15)
Grâce à cet algorithme, la solution pour 10 000 000 peut être obtenue aussi rapidement que pour 1 000. En notation de Landau, l'algorithme brute-force est O(n) et l'algorithme efficace est O(log n).
Notes et références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Project euler ».
- Portail des mathématiques
Catégorie : Enseignement des mathématiques
Wikimedia Foundation. 2010.