- Programmation non-linéaire
-
Programmation non-linéaire
En informatique, la programmation non-linéaire (ou NLP, de l'anglais : nonlinear programming) est une méthode permettant de résoudre de nombreuses équations et inéquations dépendant d'un ensemble de paramètres - on parle de « contraintes » - sous la forme d'une fonction à maximiser ou à minimiser. Cette fonction ou l'ensemble de ses paramètres peuvent être non-linéaires.
Sommaire
Formulation mathématique
On a une fonction
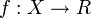, avec 
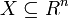. L'objectif est de déterminer le vecteur x défini par :
.
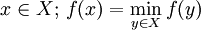De façon équivalente, on peut rechercher la valeur pour laquelle f est maximale :
.
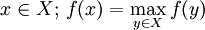Méthodes de résolution
Si la fonction est convexe ou concave, et l'ensemble des contraintes est convexe, alors il existe des méthodes spécialisées, appelées méthodes d'optimisation convexe.
Sinon, il existe plusieurs solutions. Par exemple, utilisant le principe de séparation et évaluation pour diviser et traiter séparément plusieurs paramètres.
L'algorithme peut également être arrêté avant d'aboutir, si on peut prouver qu'aucune solution ultérieure ne sera meilleure à un certain seuil de tolérance près. Les conditions de Karush-Kuhn-Tucker (KKT) garantissent qu'une solution ainsi obtenue est optimale.
Exemples
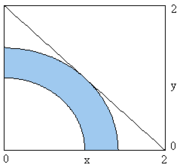
En dimension 2
L'intersection d'une ligne avec l'ensemble des contraintes représente la solution.
Un problème simple peut être posé ainsi :
- x1 ≥ 0
- x2 ≥ 0
- x12 + x22 ≥ 1
- x12 + x22 ≤ 2
où l'on cherche à maximiser la fonction
- f(x) = x1 + x2
avec x = (x1, x2)
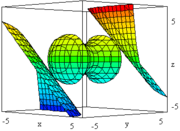
En dimension 3
L'intersection de la surface avec l'espace des contraintes au centre représente la solution.On peut formuler un problème ainsi :
- x12 − x22 + x32 ≤ 2
- x12 + x22 + x32 ≤ 10
où l'on cherche à maximiser la fonction :
- f(x) = x1x2 + x2x3
avec x = (x1, x2, x3)
Voir aussi
Articles connexes
Références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Nonlinear programming ».
- Avriel, Mordecai (2003), Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Bazaraa, Mokhtar et Shetty (1979), Nonlinear programming. Theory and algorithms. John Wiley & Sons. ISBN 0-471-78610-1.
- Nocedal, Jorge et Wright, Stephen (1999), Numerical Optimization. Springer. ISBN 0-387-98793-2.
- Bertsekas, Dimitri (1999), Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.
Liens externes
Documentation
- (en) Nonlinear programming FAQ
- (en) Mathematical Programming Glossary
- (en) Nonlinear Programming Survey OR/MS Today
Implémentations
- (en) AIMMS Optimization Modeling AIMMS — include nonlinear programming in industry solutions ;
- (en) AMPL solver software ;
- (en) GAMS General Algebraic Modeling System.
Portail de l’informatique
Catégories : Algorithme d'optimisation | Intelligence artificielle | Recherche opérationnelle
Wikimedia Foundation. 2010.
