- Problème des plus proches voisins
-
Recherche des plus proches voisins
Le problème de la recherche des plus proches voisins (ou des k plus proches voisins) est très courant en algorithmique et de nombreux auteurs ont proposé des algorithmes efficaces pour le résoudre rapidement.
Soient :
- un espace E de dimension D ;
- un ensemble A de N points dans cet espace ;
- un entier k plus petit que N.
La recherche des plus proches voisins consiste, étant donné un point x de E n'appartenant pas nécessairement à A, à déterminer quels sont les k points de A les plus proches de x. On parle alors de trouver un voisinage de taille k autour du point x.
Exemple de recherche d'un voisinage de taille 3 autour d'une coordonnée donnée (D = 1, k = 3).La recherche de voisinage est utilisée dans de nombreux domaines, tels la reconnaissance de formes, le clustering, l'approximation de fonctions, la prédiction de séries temporelles et même les algorithmes de compression (recherche d'un groupe de données le plus proche possible du groupe de données à compresser pour minimiser l'apport d'information).
Sommaire
Méthodes exactes
Recherche linéaire
L'algorithme naïf de recherche de voisinage consiste à passer sur l'ensemble des N points de A et à regarder si ce point est plus proche ou non qu'un des plus proches voisins déjà sélectionnée, et si oui, l'insérer. On obtient alors un temps de calcul linéaire en la taille de A : O(N) (tant que
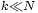). Cette méthode est appelée la recherche linéaire ou la recherche séquentielle.Algorithme naïf:
pour i allant de 1 à k mettre le point D[i] dans proches_voisins fin pour pour i allant de k+1 à N si la distance entre D[i] et x est inférieure à la distance d'un des points de proches_voisins à x supprimer de proches_voisins le point le plus éloigné de x mettre dans proches_voisins le point D[i] fin si fin pour proches_voisins contient les k plus proches voisins de xLa recherche linéaire soufre d'un problème de lenteur. Si l'ensemble A est grand, il est alors extrêmement couteux de tester les N points de l'espace.
Les optimisations de cet algorithme se basent souvent sur des cas particuliers du problème. Le plus souvent, l'optimisation consiste à effectuer au préalable un algorithme (pré-traitement) pouvant avoir une complexité supérieure à O(N) mais permettant d'effectuer par la suite très rapidement un grand nombre de recherches. Il s'agit alors de trouver un juste milieu entre le temps de pré-calculs et le nombre de recherches qui auront lieu par la suite.
Partitionnement de l'espace
Il existe des algorithmes efficaces de recherche lorsque la dimension D est petite (inférieure à ~15). La structure la plus connue est le kd-tree, introduite en 1975[1].
Un problème majeur de ces méthodes est de souffrir de la malédiction de la dimension. Lorsque la dimension D est trop grande, ces méthodes ont des performances comparables ou inférieures à une recherche linéaire[2].
Méthodes approximatives
Locality sensitive hashing
Article détaillé : Locality sensitive hashing.Voir aussi
Notes et références
- ↑ Bentley, « Multidimensional binary search trees used for associative searching », dans Comm. ACM 18, 509-517, 1975 [texte intégral]
- ↑ Piotr Indyk et Rajeev Motwani, « Approximate Nearest Neighbors: Towards Removing the Curse of Dimensionality. », dans Proceedings of 30th Symposium on Theory of Computing, 1998 [texte intégral]
Portail de l’informatique
Catégories : Algorithmique | Apprentissage automatique
Wikimedia Foundation. 2010.
