Problème de livraison et de collecte

Problème de livraison et de collecte

Problème de tournées de véhicules

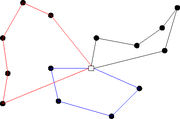
Figure illustrant un problème de tournées de véhicules avec un dépot central.

Le problème de tournées de véhicules est une classe de problèmes de recherche opérationnelle et d'optimisation combinatoire. Il s'agit de déterminer les tournées d'une flotte de véhicules afin de livrer une liste de clients[1]. Le but est de minimiser le coût de livraison des biens. Ce problème est une extension classique du problème du voyageur de commerce, et fait partie de la classe des problèmes NP-complet.

Variantes

Quelques variantes classiques du problème de tournées de véhicules:

  • Problème de tournées de véhicules avec contraintes de capacité: Les véhicules ont une capacité d'emport limitée (quantité, taille, poids, etc.).
  • Problème de tournées de véhicules avec fenêtre de temps: Pour chaque client on impose une fenêtre de temps dans laquelle la livraison doit être effectuée.
  • Problème de tournées de véhicules avec collecte et livraison: Un certain nombre de marchandise doivent être déplacées de sites de collecte vers des sites de livraisons.

La résolution du problème peut devenir très difficile lorsque les sous-problèmes interagissent entre eux, par exemple, le problème de bin packing interagit avec l'allocation et la création de tournées dans le cas d'un problème avec contraintes de capacité.

Méthodes de résolution

Comme pour la plupart des problèmes NP-complet il est difficile de résoudre des instances de grande taille de façon optimale. On se contente alors de trouver des solutions de "bonne qualité". Afin d'obtenir des solutions dans des temps de calculs raisonnable on se tourne généralement vers des méthodes approchées à base d'heuristique tel que l'algorithme de Clarke et Wright[2] pour construire une première solution que l'on améliore ensuite avec d'autres heuristiques ou des méthodes de recherche locale. On peut remarquer que les méthodes d'amélioration utilisées pour le problème du voyageur de commerce tel que l'algorithme de Lin-Kernighan [3] peuvent souvent être appliquées à chacune des tournées individuellement afin d'améliorer le coût global de la solution.

La programmation linéaire permet de résoudre de façon exacte[4] les problèmes de tournées de véhicules à l'aide de la méthode dite Branch and cut.

Références

  1. ↑ Dantzig, G.B.; Ramser, J.H. (1959). "The Truck Dispatching Problem". Management Science 6 (1): 80-91.
  2. ↑ G. Clarke and J. W. Wright. Scheduling of vehicles from a central depot to a number of delivery points. Operations Research, 12:568–581, 1964.
  3. ↑ S. Lin and B. W. Kernighan (1973). An Effective Heuristic Algorithm for the Traveling-Salesman Problem. Operations Res. 21, 498-516.
  4. ↑ D. Naddef, G. Rinaldi (2001), "Branch-and-cut algorithms for the capacitated VRP". The vehicle routing problem 53-84 ISBN:0-89871-498-2
  • Portail des mathématiques Portail des mathématiques
  • Portail de l’informatique Portail de l’informatique
Ce document provient de « Probl%C3%A8me de tourn%C3%A9es de v%C3%A9hicules ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Problème de livraison et de collecte de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Probleme de tournees de vehicules — Problème de tournées de véhicules Figure illustrant un problème de tournées de véhicules avec un dépot central. Le problème de tournées de véhicules est une classe de problèmes de recherche opérationnelle et d optimisation combinatoire. Il s agit …   Wikipédia en Français

  • Problème de tournées de véhicules — Figure illustrant un problème de tournées de véhicules avec un dépot central. Le problème de tournées de véhicules est une classe de problèmes de recherche opérationnelle et d optimisation combinatoire. Il s agit de déterminer les tournées d une… …   Wikipédia en Français

  • Économie de la Charente-Maritime — Longtemps dominée par l agriculture et des activités traditionnelles et profondément marquée par une très forte ruralité, la Charente Maritime s affranchit peu à peu de l image d un département rural et pauvre. Elle est devenue avant le début du… …   Wikipédia en Français

  • Applications des SIG — Applications des systèmes d information géographique Les Systèmes d information géographique (SIG) est une intégration organisationnelle d un logiciel et de données géographiques. Un système qui assure la collecte, le stockage, l analyse et la… …   Wikipédia en Français

  • Goguette — Le grelot de Collé et le verre de Panard, reliques emblématiques de la Société du Caveau[1] …   Wikipédia en Français

  • Chronologie de la vie d'Honoré de Balzac — Honoré de Balzac, né Honoré Balzac[1],[2],[3], à Tours le 20 mai 1799 (1er prairial an VII) et mort à Paris le 18  …   Wikipédia en Français

  • Applications des systèmes d'information géographique — Un Système d information géographique (SIG) est une intégration organisationnelle d un logiciel et de données géographiques. Autrement dit un système qui assure la collecte, le stockage, l’analyse et la visualisation de données. Les SIG aident à… …   Wikipédia en Français

  • Cinéma — Pour les articles homonymes, voir Cinéma (homonymie) et Film (homonymie). Le cinéma est un art du spectacle. Il expose au public un film, c’est à dire une œuvre composée d’images en mouvement projetées sur un support, généralement un écran blanc …   Wikipédia en Français

  • ALGÉRIE — En 1962, les fées ont été particulièrement nombreuses à se presser autour de l’Algérie. L’« exemplarité » de la lutte de libération nationale, longue et violente, ravissait ceux qui ne voient de progrès humain que dans l’action de l’« accoucheuse …   Encyclopédie Universelle

  • Risque operationnel — Risque opérationnel (établissement financier) Le risque opérationnel pour les établissements financiers (banque et de l assurance) est le risque de pertes directes ou indirectes dues à une inadéquation ou à une défaillances des procédures de l… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”