Arithmétique non-standard

Arithmétique non-standard

Arithmétique non-standard

Sommaire

Historique

Skolem fut le premier en 1922 à poser les bases de l'arithmétique non-standard.

Définition

En utilisant les axiomes de standardisation, transfert et idéalité tels que définis par Abraham Robinson, on définit les nombres hypernaturels, éléments du domaine 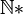\mathbb{N}*. Ces nombres hypernaturels sont standards s'ils appartiennent à \mathbb{N} et non-standards dans le cas contraire.

En logique mathématique, un modèle non-standard de l'arithmétique est un modèle du premier ordre utilisant les axiomes de Peano qui contient les nombres non-standards.Le modèle standard de l'arithmétique contient l'ensemble des nombres naturels {0, 1, 2, …}. Les éléments de chaque modèle de l'arithmétique de Peano sont ordonnés linéairement et possèdent un segment initial isomorphe aux nombres naturels standards. Un modèle non-standard est un modèle qui contient des éléments en dehors de ce segment initial.

Existence

L'existence de modèles non-standard de l'arithmétique peut être démontrée par l'application du théorème de compacité. Pour ce faire, un ensemble d'axiomes est défini dans un langage incluant le langage de l'arithmétique de Peano ainsi qu'un nouveau symbole x. L'axiome contient les axiomes de l'arithmétique de Peano en même temps qu'un autre ensemble infini d'axiomes : pour chaque naturel standard n, l'axiome x > n est inclus. Chaque sous-ensemble fini de ces axiomes vérifie le modèle standard de l'arithmétique, et donc par le théorème de compacité il y a un modèle satisfaisant tous ces axiomes. L'élément de ce modèle correspondant à x ne peut être un nombre standard.

En utilisant des méthodes plus complexes, il est possible de construire des modèles non-standard qui possèdent des propriétés plus compliquées. Par exemple, il existe des modèles de l'arithmétique de Peano dans lesquels le théorème de Goodstein n'est pas vérifié; parce qu'il peut être prouvé dans ZFC (Zermelo-Franken+axiome de choix) que le théorème de Goodstein dépend du modèle standard, modèle où l'application du théorème de Goodstein doit être non-standard.

Modèles dénombrables

On peut montrer que tout modèle non-standard dénombrable de l'arithmétique possède une structure d'ordre isomorphe à celle de 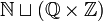\mathbb{N}\sqcup(\mathbb{Q}\times\mathbb{Z}), c'est à dire que les entiers standard sont en premier, et sont suivis d'une répartition dense de « paquets » d'entiers non standards consécutifs isomorphes à \mathbb{Z}.

On peut en effet définir la relation d'équivalence sur les entiers non standards par a équivalent à b si et seulement si a et b diffèrent d'un entier standard. On vérifie facilement qu'il s'agit d'une relation d'équivalence, que les classes d'équivalences sont isomorphes à \mathbb{Z} (en tant qu'ensembles ordonnés), et que la relation d'ordre sur les entiers du modèle passe au quotient. On montre alors que l'ensemble quotient est un ensemble ordonné sans plus grand ni plus petit élément, et dont l'ordre est dense, et comme il est dénombrable, il est isomorphe à \mathbb{Q}

Galaxie d'un hypernaturel

On appelle galaxie d'un nombre hypernaturel l'ensemble des nombres hypernaturels dont la distance ou la différence entière est naturelle :

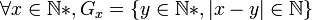
\forall x\in\mathbb{N}*,G_{x}=\{y\in\mathbb{N}*,|x-y|\in\mathbb{N}\}


Bibliographie

Liens internes

Liens externes

Ce document provient de « Arithm%C3%A9tique non-standard ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Arithmétique non-standard de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Arithmétique non standard — En logique mathématique, un modèle non standard de l arithmétique est un modèle du premier ordre utilisant les axiomes de Peano qui contient les nombres non standards. Le modèle standard de l arithmétique contient l ensemble des nombres naturels… …   Wikipédia en Français

  • non standard — ● non standard adjectif Qui ne répond pas aux canons d un modèle habituel, aux normes courantes d un appareil. ● non standard (expressions) adjectif Analyse ou mathématique non standard, domaine des mathématiques développé en 1966 par A. Robinson …   Encyclopédie Universelle

  • Modele non standard — Modèle non standard Dans la théorie des modèles, un modèle non standard est un modèle dont l ensemble de base est différent (plus large) que le modèle standard . Les propositions qui sont vraies dans le modèle standard sont vraies dans le modèle… …   Wikipédia en Français

  • Modèle Non Standard — Dans la théorie des modèles, un modèle non standard est un modèle dont l ensemble de base est différent (plus large) que le modèle standard . Les propositions qui sont vraies dans le modèle standard sont vraies dans le modèle non standard (par sa …   Wikipédia en Français

  • Modèle non standard — En logique mathématique, plus précisément en théorie des modèles, un modèle non standard est un modèle dont l ensemble de base est différent du modèle standard . Les propositions qui sont vraies dans le modèle standard sont vraies dans le modèle… …   Wikipédia en Français

  • Analyse ou mathématique non standard — ● Analyse ou mathématique non standard domaine des mathématiques développé en 1966 par A. Robinson, visant à étendre les règles de l arithmétique à des nombres « infiniment grands » ou « infiniment petits ». (L analyse non standard renouvelle l… …   Encyclopédie Universelle

  • Arithmétique de Peano — Axiomes de Peano Les axiomes de Peano sont, en mathématiques, un ensemble d axiomes de second ordre proposés par Giuseppe Peano pour définir l arithmétique[1]. Sommaire 1 Axiomes 2 Arithmétique de Peano …   Wikipédia en Français

  • Arithmetique modulaire — Arithmétique modulaire Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un… …   Wikipédia en Français

  • Arithmétique Modulaire — Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes… …   Wikipédia en Français

  • Arithmétique modulaire (synthèse) — Arithmétique modulaire Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”