- Partiel (acoustique)
-
Pour les articles homonymes, voir Partiel.
Premiers partiels d'une corde vibrante, correspondant à ses harmoniques
En acoustique musicale, un partiel désigne une des fréquences d'un instrument de musique. La somme des harmoniques donne le timbre d'un instrument. Il y a lieu de savoir qu'un partiel n'est pas la même chose qu'un harmonique.
Sons harmoniques
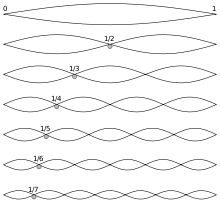
Tout phénomène périodique (et de durée infinie) peut être décomposé en une série de fréquences, dite série de Fourier, série composée d'une fondamentale et de fréquences multiples de cette fondamentale.
En acoustique, il y a deux systèmes différents pour nommer ces composantes de fréquence sinusoïdale d'un son périodique.
- Considérant le spectre sonore dans son entier, la fréquence fondamentale f0 est également appelée premier partiel.
- Avec un son musical de hauteur fixe, il est plus commode d'utiliser la notion d'harmoniques. f0 est la fondamentale, et f1 (= 2 x f0) le second harmonique, etc.
Mais la véritable justification de la décomposition de Fourier en acoustique est que le son, synthétisé à partir de la superposition des harmoniques calculés, possède un timbre indifférenciable de celui du son d'origine.
D'une façon générale, il est préférable de réserver le terme « harmonique » aux sons musicaux strictement périodiques et infinis, dont les composantes spectrales sont des multiples entiers de la fréquence fondamentale. Dans tous les autres cas, où les « fréquences harmoniques » du son ne sont plus des multiples entiers de la fréquence la plus basse, il serait illogique d'appeler ces fréquences supérieures « harmoniques inharmoniques » ; c'est pourquoi on parle alors uniquement de partiels. Par exemple, les instruments à percussion, instruments qui n'ont pas de hauteur fixe, ne comportent que des partiels. Les transitoires d'attaque, c'est-à-dire des composantes du son qui ne sont pas périodiques et de durée infinie, tel un claquement, un choc, le crissement de la colophane sur la corde d'un violon au tout début du son, sont tous des phénomènes inharmoniques qui ne peuvent se décomposer qu'en partiels. Ces phénomènes, échappant à la stricte décomposition de Fourier, sont néanmoins accessibles à son extension plus moderne, la transformée de Fourier.
Annexes
Articles connexes
Wikimedia Foundation. 2010.
