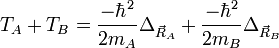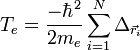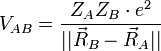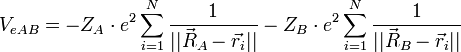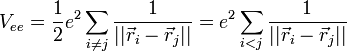Approximation De Born-Oppenheimer

Approximation De Born-Oppenheimer: Approximation de Born-Oppenheimer

En chimie quantique, le calcul des niveaux d'énergie et des fonctions d'onde d'une molécule (même de taille modeste) est une tâche extrêmement lourde. L'approximation de Born-Oppenheimer (BO) permet de la soulager grandement. Cette méthode a été publiée en 1927 par Born et Oppenheimer et est toujours utilisée en chimie quantique.

L'hypothèse de Born et Oppenheimer peut s'exprimer ainsi : on considère que l'on peut découpler le mouvement des électrons de celui des noyaux, en estimant que leur mouvement est beaucoup plus lent que celui des électrons : on les considère comme fixes dans l'étude du mouvement des électrons de la molécule. On traite alors les distances internucléaires comme des paramètres. Elle a une conséquence calculatoire immédiate, qu'on appelle hypothèse adiabatique. Il s'agit en fait de la même approximation.

Pour fixer le contexte de cette méthode, considérons l'interaction coulombienne d'un proton et d'un électron. Ce problème est celui de l'atome d'hydrogène. On peut toujours ramener l'étude du mouvement de deux corps (formant un système isolé) dans le référentiel du laboratoire à celui d'un seul corps, dit "mobile fictif", dans le référentiel du centre de masse, centre de masse en translation rectiligne uniforme dans le laboratoire. Le centre de masse est ici pratiquement confondu avec le proton puisque la masse d'un proton ( $m p$ de l'ordre de $1,67.10 - 27$ kg) est environ 1800 fois plus grande que celle de l'électron ( $m e$ de l'ordre de $9,31.10 - 31$ kg). Par ailleurs, la masse µ du mobile fictif est pratiquement celle de l'électron : 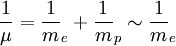$\frac 1 \mu= \frac 1 m_e + \frac 1 m_p\sim \frac 1 m_e$ . On est donc ramené à l'étude du mouvement de la particule fictive (dont la masse µ est pratiquement celle de l'électron) dans le référentiel du centre de masse (où le proton est pratiquement immobile). Dans ce contexte, la résolution analytique exacte (*) de l'équation de Schrödinger pour l'atome d'hydrogène est possible.

L'idée de l'approximation BO est inspirée de cette étude, à cette différence importante près que le problème de l'atome d'hydrogène est un problème à deux corps, analytiquement exactement soluble, alors que celui d'une molécule est un problème à au moins trois corps, insoluble analytiquement sans approximations. Même la molécule la plus simple qui soit, l'ion moléculaire 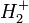$H_2^+$ est un problème à 3 corps. C'est le fait que les noyaux sont beaucoup plus lourds que les électrons qui est exploité ici : la méthode du mobile fictif nous a simplement permis de nous assurer qu'étudier le mouvement d'un électron en fixant la position du noyau est une bonne approximation, dans l'étude de l'atome d'hydrogène. Il en est de même pour le mouvement des électrons d'une molécule.

(*) : le fait de considérer µ comme étant pratiquement la masse de l'électron et le centre de masse comme étant pratiquement confondu avec le proton, n'est pas nécessaire à la résolution exacte. Ce sont des approximations numériques qui n'affectent pas le principe de la résolution. Le point important, qui permet, en pratique, l'étude exacte de l'atome d'hydrogène est la possibilité de ramener un problème à 2 corps à un problème à un corps.

Sommaire

1 Application à une molécule diatomique

1.1 Principe

1.2 Application

1.2.1 Hamiltonien d'une molécule diatomique A-B

1.2.2 Equation de Schrödinger électronique

1.2.3 Equation de Schrödinger nucléaire

1.3 Conclusion

2 Voir aussi

3 Notes et références

3.1 Liens externes

Application à une molécule diatomique

Principe

On peut résumer les deux étapes de la méthode pour une molécule diatomique, dont les noyaux, qui sont considérés comme ponctuels vis-à-vis de l'étendue du mouvement des électrons, sont distants d'un longueur R :

1) On étudie d'abord le mouvement des électrons dans une configuration nucléaire donnée, où la distance internucléaire R est considérée comme fixe (il est équivalent de dire que les deux noyaux sont fixes) ; l'approximation de Born-Oppenheimer consiste à dire que cette hypothèse fournira des solutions correctes, bien que non-exactes. On résout alors l'équation de Schrödinger pour les électrons en traitant R comme un paramètre. On obtient un ensemble 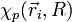${\chi_p(\vec r_i, R)}$ d'états propres pour le système électronique, d'énergies $E p (R)$ . Les N électrons de la molécule sont repérés par leur rayon-vecteur 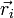$\vec r_i$ , où $i = 1,2,..., N$ . Ces états forment une base de l'espace des états du système électronique, appelée base adiabatique. On écrira qu'en fait, la fonction d'onde totale de la molécule se développe sur cette base. Au cours du calcul, on utilise une autre hypothèse, dite adiabatique, selon laquelle les électrons, très mobiles par rapport aux noyaux, ajustent instantanément leur état aux variations de l'état du système de noyaux.

2) On étudie ensuite le mouvement des deux noyaux (rotation et vibration de "l'haltère" formée par les deux noyaux), indépendamment de l'état du système électronique. Un point important est que les énergies $E p (R)$ trouvées à la première étape apparaîtront comme un terme supplémentaire dans la partie d'énergie potentielle du hamiltonien du système de noyaux. Cette étude ne relève plus directement de l'approximation de Born-Oppenheimer. Il ne faut cependant pas perdre de vue que l'étude de la vibration et de la rotation des molécules se fait dans le contexte préparé par cette approximation. Dans la pratique, tout ce qui est dit sur cette page se résume au fait que l'on étudie par la suite la rotation et la vibration d'une molécule dans un état électronique donné, représenté par une courbe d'énergie potentielle.

Application

Hamiltonien d'une molécule diatomique A-B

On considère une molécules formée de deux atomes, A et B, de masse $m A$ et $m B$ , de numéro atomique $Z A$ et $Z B$ . Ces deux atomes apportent un total de N électrons, chacun de charge -q, repérés par un indice i. On a $N = Z A + Z B$ si la molécule est électriquement neutre. Le calcul mené ci-dessous se place dans ce cas ; par exemple $Z A$ est aussi bien le nombre de protons du noyau de A que son nombre d'électrons. Le hamiltonien doit comporter l'énergie cinétique des noyaux $T A$ et $T B$ , l'énergie cinétique des électrons $T e$ , l'énergie potentielle d'interaction électrostatique des noyaux entre eux $V A B$ , des électrons entre eux $V e e$ , des électrons et des noyaux $V e A B$ . On a donc
$H = T A + T B + T e + V A B + V e A B + V e e$
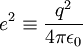
où, avec $e^2\equiv \frac{q^2}{4\pi\epsilon_0}$

$T_A+T_B=\frac{-\hbar^2}{2m_A}\Delta_{\vec R_A} + \frac{-\hbar^2}{2m_B}\Delta_{\vec R_B}$

$T_{e}=\frac{-\hbar^2}{2m_e}\sum_{i=1}^N\Delta_{\vec r_i}$

$V_{AB}=\frac{Z_A Z_B \cdot e^2}{||\vec R_B - \vec R_A||}$

$V_{e A B}=-Z_A\cdot e^2 \sum_{i=1}^N \frac{1}{||\vec R_A - \vec r_i||}-Z_B\cdot e^2 \sum_{i=1}^N \frac{1}{||\vec R_B - \vec r_i||}$

$V_{e e}=\frac{1}{2}e^2\sum_{i\neq j}\frac{1}{||\vec r_i - \vec r_j||}=e^2\sum_{i<j}\frac{1}{||\vec r_i - \vec r_j||}$

On se place maintenant dans le référentiel du centre de masse G des noyaux, et on prend G pour origine des positions. Remarquons qu'il n'est pas exactement confondu avec le centre de masse de la molécule. L'énergie cinétique des noyaux dans le référentiel du laboratoire est, comme en mécanique classique, la somme de l'énergie cinétique du centre de masse dans ce référentiel et de l'énergie cinétique des noyaux dans le référentiel du centre de masse (RCM). On sait (voir un cours de mécanique classique) que dans le RCM, l'étude du mouvement des deux noyaux peut être ramené à celui du mobile fictif dont la position est donnée par 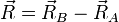$\vec R = \vec R_B - \vec R_A$ , et dont la masse est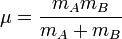 $\mu=\frac{m_Am_B}{m_A+m_B}$

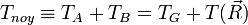
Dans le référentiel du laboratoire : $T_{noy}\equiv T_A+T_B=T_G+T(\vec R)$

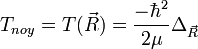
Dans le RCM : $T_{noy}=T(\vec R)=\frac{-\hbar^2}{2\mu}\Delta_{\vec R}$

Les autres termes du hamiltonien ne sont pas modifiés dans le RCM, en se rappelant toutefois que les positions sont maintenant repérées par rapport au centre de masse de A et B.

Equation de Schrödinger électronique

L'équation de Schrödinger dont la fonction d'onde totale 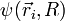$\psi(\vec r_i, R)$ de la molécule est solution s'écrit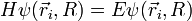
$H\psi(\vec r_i, R)=E\psi(\vec r_i, R)$
où, d'après BO, les mouvements électronique et nucléaire sont découplés, et au sein du mouvement nucléaire les mouvements de rotation et de vibration le sont également :

$E = E e l e c t r o n i q u e + E v i b r a t i o n + E r o t a t i o n$

et

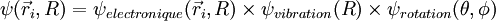
$\psi(\vec r_i, R)=\psi_{electronique}(\vec r_i, R)\times\psi_{vibration}(R)\times\psi_{rotation}(\theta,\phi)$

L'approximation BO stipule que les noyaux sont fixes dans le RCM : $T n o y = 0$

Dans le hamiltonien, il ne reste donc plus que des termes électroniques : c'est un hamiltonien dont la solution est la fonction d'onde électronique 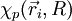$\chi_p(\vec r_i, R)$ décrivant le système d'électrons de la molécule :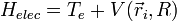

$H_{elec}=T_{e}+V(\vec r_i, R)$

où l'on a rassemblé les termes d'énergie potentielle énumérés ci-dessus dans le terme 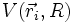$V(\vec r_i, R)$ . Remarquons que l'on y a inclus (par convention) le terme de répulsion coulombienne des noyaux entre eux $V A B$ . Ce n'est pas un terme d'énergie électronique, mais il est traité comme une constante puisque ne dépendant que de la distance entre noyaux qui est elle-même traitée comme un paramètre dans l'approximation de Born-Oppenheimer.

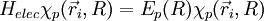
On a donc $H_{elec}\chi_p(\vec r_i, R)=E_p(R)\chi_p(\vec r_i, R)$

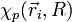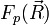On suppose que la fonction d'onde totale de la molécule se développe sur la base ${\chi_p(\vec r_i, R)}$ . Les coefficients du développement sont notés $F_p(\vec R)$ .

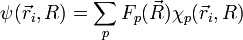
$\psi(\vec r_i,R)=\sum_p F_p(\vec R)\chi_p(\vec r_i, R)$
expression que l'on réinjecte dans l'équation de Schrödinger initiale, avant l'hypothèse BO :
$\left[T_{noy}+H_{elec}\right]\sum_p F_p(\vec R)\chi_p(\vec r_i, R)=E\sum_p F_p(\vec R)\chi_p(\vec r_i, R)$
donc par action de $H e l e c$ :
$\left[T_{noy}+E_p(R)\right]\sum_p F_p(\vec R)\chi_p(\vec r_i, R)=E\sum_p F_p(\vec R)\chi_p(\vec r_i, R)$
expression que l'on projette sur une fonction 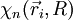$\chi_n(\vec r_i, R)$ donnée de la base adiabatique :

$\sum_p\int d^3r_1 ... d^3r_N \chi_n^*(\vec r_i, R)T_{noy} \left[ F_p(\vec R)\chi_p(\vec r_i, R)\right ]+E_n(R)F_n(\vec R)=EF_n(\vec R)$
puisque la base adiabatique est orthonormée.

Hypothèse adiabatique

On connaît l'action de 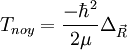$T_{noy}=\frac{-\hbar^2}{2\mu}\Delta_{\vec R}$ dans le RCM, donc :

$T_{noy} \left[ F_p(\vec R)\chi_p(\vec r_i, R)\right ]=\frac{-\hbar^2}{2\mu}\Delta_{\vec R}\left[ F_p(\vec R)\chi_p(\vec r_i, R)\right ]$

i.e.

$T_{noy} \left[ F_p(\vec R)\chi_p(\vec r_i, R)\right ]=\frac{-\hbar^2}{2\mu}\left[ F_p(\vec R)\Delta_{\vec R}\chi_p(\vec r_i, R)+2\vec\nabla_{\vec R}F_p(\vec R)\vec\nabla_{\vec R}\chi_p(\vec r_i, R)+\chi_p(\vec r_i, R)\Delta_{\vec R}F_p(\vec R)\right ]$

L'approximation adiabatique consiste à dire que les variations de la fonction d'onde électronique 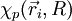$\chi_p(\vec r_i, R)$ lors d'une petite variation de 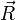$\vec R$ sont négligeables devant celles du coefficient 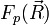$F_p(\vec R)$ . Ainsi, les deux premiers termes de la somme ci-dessus sont négligés :

$T_{noy} \left[F_p(\vec R)\chi_p(\vec r_i, R)\right]=\frac{-\hbar^2}{2\mu}\left[\chi_p(\vec r_i, R)\Delta_{\vec R}F_p(\vec R)\right ]$

Réécrivons alors l'expression obtenue après projection sur $χ n$ , en tenant compte du calcul précédent :

$\sum_p\int d^3r_1 ... d^3r_N \chi_n^*(\vec r_i, R)\frac{-\hbar^2}{2\mu}\left[\chi_p(\vec r_i, R)\Delta_{\vec R}F_p(\vec R)\right ]+E_n(R)F_n(\vec R)=EF_n(\vec R)$
et puisque la base adiabatique est orthonormée : 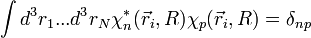$\int d^3r_1 ... d^3r_N \chi_n^*(\vec r_i, R)\chi_p(\vec r_i, R)=\delta_{np}$ , donc :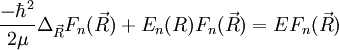

$\frac{-\hbar^2}{2\mu}\Delta_{\vec R}F_n(\vec R)+E_n(R)F_n(\vec R)=EF_n(\vec R)$
qu'on peut réécrire comme suit :
$\left[\frac{-\hbar^2}{2\mu}\Delta_{\vec R}+E_n(R)\right ]F_n(\vec R)=EF_n(\vec R)$
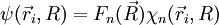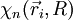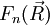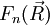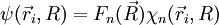qui apparaît comme l'équation de Schrödinger dont $\psi(\vec r_i,R)=F_n(\vec R)\chi_n(\vec r_i, R)$ est solution, dans le cadre de l'hypothèse adiabatique (dans laquelle $\chi_n(\vec r_i, R)$ se comporte comme un scalaire multipliant $F_n(\vec R)$ , sous l'action du laplacien. On peut donc remplacer $F_n(\vec R)$ par $\psi(\vec r_i,R)=F_n(\vec R)\chi_n(\vec r_i, R)$ ).

Ainsi, l'approximation adiabatique a permis de ramener un état de la molécule, initialement décrit comme une superposition de fonctions de la base adiabatique, à une seule de ces fonctions.

Equation de Schrödinger nucléaire

Nous amorçons ici l'étude de la rotation et de la vibration de la molécule diatomique. Reprenons la dernière équation ci-dessus. Nous pouvons l'interpréter comme étant l'équation de Schrödinger nucléaire, où le terme d'énergie cinétique est bien celui du mobile fictif correspondant au mouvement relatif des noyaux (c'est l'énergie cinétique totale des noyaux dans le référentiel du centre de masse), et où la valeur propre $E n (R)$ du hamiltonien électronique joue le rôle d'une énergie potentielle dans ce hamiltonien nucléaire.

Cette énergie est une fonction radiale, et les résultats relatifs au mouvement dans un potentiel central, obtenus traditionnellement dans l'étude quantique de l'atome d'hydrogène s'appliquent : on peut développer 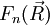$F_n(\vec R)$ comme produit d'une fonction radiale et d'une fonction angulaire sous la forme

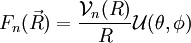
$F_n(\vec R)=\frac{\mathcal V_n(R)}{R}\mathcal U(\theta, \phi)$
La fonction 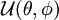$\mathcal U(\theta, \phi)$ décrit la rotation de la molécule. La fonction 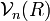$\mathcal V_n(R)$ décrit la vibration de la molécule. En reportant l'expression de 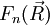$F_n(\vec R)$ dans l'équation de Schrödinger et en écrivant l'action du laplacien (décomposé en partie radiale et partie angulaire), on obtient l'équation radiale dont 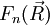$F_n(\vec R)$ est solution et qui fournit les niveaux d'énergie de vibration, et l'équation angulaire dont 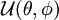$\mathcal U(\theta, \phi)$ est solution et qui fournit les niveaux d'énergie de rotation. Les résultats obtenus pour la rotation et la vibration reposent sur le choix du potentiel électronique $E n (R)$ .

Conclusion

L'énergie totale de la molécule dans le référentiel du centre de masse apparaît in fine comme la somme de l'énergie électronique, de l'énergie de rotation de "l'haltère" formée par les noyaux (rotateur rigide) et de l'énergie de vibration des noyaux (l'image correspondante est celle de "masses ponctuelles reliées par un ressort". En physique nucléaire, on parle aussi d'énergie de rotation et de vibration des noyaux, dans le cadre d'un modèle dit collectif ; le noyau y est considéré comme un objet non ponctuel). On a donc découplage de la rotation des noyaux, de la vibration des noyaux, et du mouvement des électrons. Ce résultat simple et important est la conséquence du l'approximation de Born-Oppenheimer. Ce modèle élémentaire est amélioré en considérant par exemple le couplage de la rotation et de la vibration comme une perturbation au mouvement idéal découplé (distorsion centrifuge).

Voir aussi

Atome d'hydrogène

Approximation orbitale

Notes et références

Mécanique Quantique, tomes 1 et 2 - Cohen Tannoudji, Diu, Laloë (Hermann)

Physique Atomique, tome 2, seconde édition - Cagnac, Tchang-Brillet, Pebay-Peyroula (Dunod)

Atoms and molecules : an introduction for students of physical chemistry - Karplus, Porter (Cummings Publishing Company)

Physics of Atoms and Molecules - Bransden, Joachain (Prentice-Hall)

Liens externes

Article original de Born et Oppenheimer (in Annalen der Physik, 1927) (en allemand)

Traduction en anglais par H. Hettema

Traduction en anglais par S. M. Blinder

Portail de la physique

Portail de la chimie

Ce document provient de « Approximation de Born-Oppenheimer ».

Catégories : Physique quantique | Chimie quantique

Contenu soumis à la licence CC-BY-SA. Source : Article Approximation De Born-Oppenheimer de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Approximation de born-oppenheimer — En chimie quantique, le calcul des niveaux d énergie et des fonctions d onde d une molécule (même de taille modeste) est une tâche extrêmement lourde. L approximation de Born Oppenheimer (BO) permet de la soulager grandement. Cette méthode a été… … Wikipédia en Français
Approximation de Born-Oppenheimer — Ne pas confondre avec Born approximation (en) En chimie quantique, le calcul des niveaux d énergie et des fonctions d onde d une molécule (même de taille modeste) est une tâche extrêmement lourde. L approximation de Born Oppenheimer… … Wikipédia en Français
approximation de Born-Oppenheimer — Borno ir Openheimerio artinys statusas T sritis fizika atitikmenys: angl. Born Oppenheimer approximation vok. Born Oppenheimer Näherung, f rus. приближение Борна Оппенгеймера, n pranc. approximation de Born Oppenheimer, f … Fizikos terminų žodynas
Approximation Born-Oppenheimer — Approximation de Born Oppenheimer En chimie quantique, le calcul des niveaux d énergie et des fonctions d onde d une molécule (même de taille modeste) est une tâche extrêmement lourde. L approximation de Born Oppenheimer (BO) permet de la… … Wikipédia en Français
Born-Oppenheimer — Approximation de Born Oppenheimer En chimie quantique, le calcul des niveaux d énergie et des fonctions d onde d une molécule (même de taille modeste) est une tâche extrêmement lourde. L approximation de Born Oppenheimer (BO) permet de la… … Wikipédia en Français
Born-Oppenheimer approximation — Borno ir Openheimerio artinys statusas T sritis fizika atitikmenys: angl. Born Oppenheimer approximation vok. Born Oppenheimer Näherung, f rus. приближение Борна Оппенгеймера, n pranc. approximation de Born Oppenheimer, f … Fizikos terminų žodynas
Born-Oppenheimer Näherung — Borno ir Openheimerio artinys statusas T sritis fizika atitikmenys: angl. Born Oppenheimer approximation vok. Born Oppenheimer Näherung, f rus. приближение Борна Оппенгеймера, n pranc. approximation de Born Oppenheimer, f … Fizikos terminų žodynas
Born-Oppenheimer approximation — In quantum chemistry, the computation of the energy and wavefunction of an average size molecule is a formidable task that is alleviated by the Born Oppenheimer (BO) approximation. For instance the benzene molecule consists of 12 nuclei and 42… … Wikipedia
Born-Oppenheimer-Approximation — Die Born Oppenheimer Näherung oder Born Oppenheimer Approximation oder adiabatische Näherung ist eine Methode zur Lösung der Schrödingergleichung für ein System mit mehreren schweren und wenigstens einem leichten Teilchen. Dieses Problem tritt… … Deutsch Wikipedia
Born- Oppenheimer- Näherung — Die Born Oppenheimer Näherung oder Born Oppenheimer Approximation oder adiabatische Näherung ist eine Methode zur Lösung der Schrödingergleichung für ein System mit mehreren schweren und wenigstens einem leichten Teilchen. Dieses Problem tritt… … Deutsch Wikipedia

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts