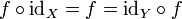- Application identique
-
Application identité
Pour les articles homonymes, voir Identité.En mathématiques, sur un ensemble X donné, une application identité ou fonction identité est une application qui n'a aucun effet lorsqu'elle est appliquée à un élément : elle renvoie toujours la valeur qui est utilisée comme argument :
.
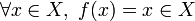Le graphe de l'application identité est appelée la diagonale de l'espace produit
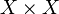. Pour 
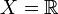, l'ensemble des nombres réels, le graphe est la première bissectrice du plan euclidien.Notations
L'application identité sur X est notée idX ou IdX. quand il n'y a pas d'ambiguïté sur l'ensemble sur lequel on travaille, on note l'application identité id ou Id.
Elle est parfois notée 1X, mais cette dernière notation peut prêter à confusion avec la fonction indicatrice d'une partie A d'un ensemble X.
Propriétés remarquables
Pour toute application d'un ensemble X dans un ensemble Y, on a :
En particulier, l'application identité est l'élément neutre du monoïde des applications de X dans lui-même.
L'application identité est une bijection de X dans lui-même.
L'ensemble des bijections d'un ensemble X dans lui-même, muni de la composition de fonctions, constitue un groupe (appelée groupe symétrique) non vide, dont l'application identité est l'élément neutre.
En topologie
L'application identité permet de comparer deux topologies : Soient deux topologies T et T' définies sur un même ensemble E. Si l'application identité de (E,T) dans (E,T') est continue, on dit que la topologie T est plus fine que T'.
Portail des mathématiques
Catégories : Fonction remarquable | Théorie des ensembles
Wikimedia Foundation. 2010.
