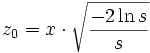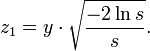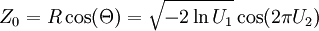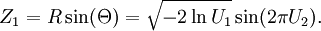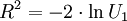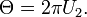Méthode De Box-Muller

Méthode de Box-Muller

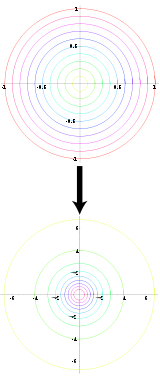Représentation graphique de la transformation : les cercles de départ, répartis uniformément autour de l'origine, deviennent un nouvel ensemble de cercles centrés, dont la répartition est proche de l'origine puis s'étiole rapidement. Les plus grands cercles de départ correspondent aux plus petits cercles d'arrivée, et vice-versa.

La méthode de Box-Muller (George Edward Pelham Box et Mervin Edgar Muller, 1958) consiste à générer des paires de nombres aléatoires à distribution normale centrée réduite, à partir d'une source de nombres aléatoires de loi uniforme.

La transformation prend communément deux formes.

La forme simple transforme des coordonnées cartésiennes uniformément distribuées dans le cercle unité en des coordonnées normalement distribuées.
La forme polaire transforme des coordonnées polaires uniformément distribuées en des coordonnées cartésiennes normalement distribuées.

On peut également utiliser la méthode de la transformée inverse pour générer des nombres normalement distribués; la méthode de Box-Muller a été mise au point pour être algorithmiquement plus efficiente^[1]. On peut également envisager la Méthode Ziggourat qui est aussi très efficiente.

Forme cartésienne

Soient x et y choisis indépendamment et uniformément dans [−1,1], et s = x² + y². Si s > 1, rejetons-le et choisissons à nouveau un couple (x, y), jusqu'à ce que s appartienne à ]0,1]. Pour ces points "filtrés", calculons ensuite:

$z_0 = x \cdot \sqrt{\frac{-2 \ln s}{s}}$

$z_1 = y \cdot \sqrt{\frac{-2 \ln s}{s}}.$

Forme polaire

Soient $U 1$ et $U 2$ deux variables aléatoires indépendantes uniformément distribuées dans ]0,1].

Soient

$Z_0 = R \cos(\Theta) =\sqrt{-2 \ln U_1} \cos(2 \pi U_2)\,$

$Z_1 = R \sin(\Theta) = \sqrt{-2 \ln U_1} \sin(2 \pi U_2).\,$

Alors Z₀ et Z₁ sont des variables aléatoires indépendantes suivant une loi normale de variance 1.

Cette transformation ^[2] vient du fait que, dans un système cartésien à deux dimensions où les coordonnées X et Y suivent deux variables aléatoires indépendantes normales, les variables aléatoires R² et $Θ$ (ci-dessus) sont également indépendantes et peuvent s'écrire

$R^2 = -2\cdot\ln U_1\,$

$\Theta = 2\pi U_2.\,$

Comparaison entre les deux formes

La forme cartésienne est une méthode d'échantillonnage à rejet, qui n'utilise qu'une partie des nombres générés par la source aléatoire, mais elle est en pratique plus rapide que la forme polaire car elle est plus simple à calculer:

la forme cartésienne n'utilise pas de fonctions trigonométriques, coûteuses en temps de calcul
la génération de nombres aléatoires est plutôt rapide, il n'est donc pas gênant d'en gaspiller une partie. En moyenne la part de points rejetés est (1-π/4) ≈ 21.46%. On génère donc 4/π ≈ 1.2732 nombres aléatoires uniformes pour obtenir chaque nombre aléatoire normal.

Notes

↑ Kloeden and Platen, Numerical Solutions of Stochastic Differential Equations, p. 11-12
↑ Sheldon Ross, A First Course in Probability, (2002), p.279-81

Ce document provient de « M%C3%A9thode de Box-Muller ».

Catégorie : Nombre aléatoire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode De Box-Muller de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Methode de Box-Muller — Méthode de Box Muller Représentation graphique de la transformation : les cercles de départ, répartis uniformément autour de l origine, deviennent un nouvel ensemble de cercles centrés, dont la répartition est proche de l origine puis s… … Wikipédia en Français
Méthode de box-muller — Représentation graphique de la transformation : les cercles de départ, répartis uniformément autour de l origine, deviennent un nouvel ensemble de cercles centrés, dont la répartition est proche de l origine puis s étiole rapidement. Les… … Wikipédia en Français
Méthode de Box-Muller — Représentation graphique de la transformation : les cercles de départ, répartis uniformément autour de l origine, deviennent un nouvel ensemble de cercles centrés, dont la répartition est proche de l origine puis s étiole rapidement. Les… … Wikipédia en Français
Box-Muller — Méthode de Box Muller Représentation graphique de la transformation : les cercles de départ, répartis uniformément autour de l origine, deviennent un nouvel ensemble de cercles centrés, dont la répartition est proche de l origine puis s… … Wikipédia en Français
Box-Müller-Methode — Graphische Veranschaulichung der Box Muller Methode Die Box Muller Methode (nach George Edward Pelham Box und Mervin Edgar Muller 1958) ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen. Inhaltsverzeichnis 1 Idee … Deutsch Wikipedia
Box-Muller-Algorithmus — Graphische Veranschaulichung der Box Muller Methode Die Box Muller Methode (nach George Edward Pelham Box und Mervin Edgar Muller 1958) ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen. Inhaltsverzeichnis 1 Idee … Deutsch Wikipedia
Box-Muller-Transformation — Graphische Veranschaulichung der Box Muller Methode Die Box Muller Methode (nach George Edward Pelham Box und Mervin Edgar Muller 1958) ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen. Inhaltsverzeichnis 1 Idee … Deutsch Wikipedia
Box-Muller-Verfahren — Graphische Veranschaulichung der Box Muller Methode Die Box Muller Methode (nach George Edward Pelham Box und Mervin Edgar Muller 1958) ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen. Inhaltsverzeichnis 1 Idee … Deutsch Wikipedia
Box-Muller-Methode — Graphische Veranschaulichung der Box Muller Methode Die Box Muller Methode (nach George Edward Pelham Box und Mervin Edgar Muller 1958) ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen. Inhaltsverzeichnis 1 … Deutsch Wikipedia
Transformation de Box-Muller — Méthode de Box Muller Représentation graphique de la transformation : les cercles de départ, répartis uniformément autour de l origine, deviennent un nouvel ensemble de cercles centrés, dont la répartition est proche de l origine puis s… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Méthode De Box-Muller