Modèle de haser

Modèle de haser

Modèle de Haser

Le modèle de Haser[1] est très souvent utilisé pour interpréter les résultats d'observation des comètes. Supposant une forme sphérique du noyau, ce modèle permet de donner une estimation correcte et rapide de quantité d'eau (ou autres molécules présentes) produite par la comète sous l'influence du rayonnement solaire.

Sommaire

Présentation

Présenté en 1957 dans le Bulletin de l'académie royale de Belgique par L. Haser ce fut le premier modèle cométaire sur la distribution radiale des molécules dans la tête d'une comète. La distribution théorique des densités y fut présentée. On y tient compte des molécules issues directement du noyau (molécules mères) par évaporation, ainsi que des molécules filles, issues de la photo-dissociation de ces premières. Ce modèle se base sur des hypothèses simples. Il a l'avantage de fournir des estimations du taux de production des différentes composants, notamment d'eau le constituant essentiel du noyau. Le tout sans imbriquer beaucoup de paramètres physiques dans les calculs.

Hypothèses

  • Le noyau de la comète de rayon rn a une forme sphérique ; sa substance s'évapore sous l'influence de radiation solaire.
  • Les molécules s'échappent du noyau dans toutes les directions avec une vitesse radiale vp constante.
  • Les molécules sont désintégrées par photo-dissociation suivant la loi
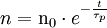
n = \mathrm n_0 \cdot e ^{-\frac{t}{\tau_p}}

n0 : est le nombre de molécules au temps t = 0;

τp: est la durée de vie d'une molécule mère
  • Les molécules filles sont elles-mêmes détruites par le rayonnement solaire.
  • Lors de la dissociation, la vitesse d'éjection fournie est dans la direction radiale aussi.


Distribution radiale pour les molécules-mères

On assimile le taux de production de l'eau Qp au flux de molécules à la surface. On a alors : Qp = Φ(0) La symétrie est sphérique, la vitesse est parallèle à la normale de la surface. On obtient le flux au point r par intégration de la quantité 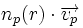n_p(r) \cdot \overrightarrow {v_p} sur la sphère de rayon r: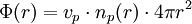

\Phi (r) = v_p \cdot n_p(r) \cdot 4\pi r ^2

Le flux Φ(r) n'est pas conservatif, car la population suit la loi en décroissance exponentielle. A une distance r du noyau la valeur du flux devient :

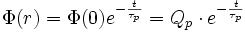
\Phi(r) = \Phi(0) e ^{-\frac{t}{\tau_p}} = Q_p \cdot e ^{-\frac{t}{\tau_p}}

La distribution radiale de densité de molécules mères est donc :

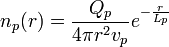
n_p (r) = \frac{Q_p}{4\pi r ^2 v_p} e ^ {-\frac{ r }{L_p}}

C'est la formule de Haser pour les molécules-mères.

Distribution des molécules-filles

Soit Np(rn) le nombre de molécules qui s'échappent du noyau par seconde et par unité de surface et Np(X)la même quantité à la distance X du centre du noyau. En tenant compte de la loi de décroissance de population le nombre total de molécules qui traversent une sphère de rayon X est alors

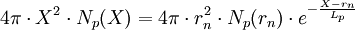
4\pi \cdot X ^2 \cdot N_p(X) = 4\pi \cdot r_n ^2 \cdot N_p (r_n) \cdot e ^ {-\frac{X-r_n}{L_p}}

Où 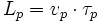L_p = v_p \cdot \tau_p , est la longueur d'échelle de la molécule mère. On en déduit le nombre de molécules filles(f) formées dans une coquille d'épaisseur dX :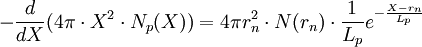

-\frac{d}{dX}(4\pi \cdot X ^2 \cdot N_p (X)) = 4\pi r_n ^2 \cdot N(r_n) \cdot \frac{1}{L_p} e ^ {-\frac{X-r_n}{L_p}}

Quand ces molécules, produites à la distance X du noyau, atteignent la distance r leur nombre est réduit sous l'influence du rayonnement solaire. Le facteur de réduction est 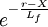e ^{-\frac{r -X}{L_{f}}} . Lf est la longueur d'échelle de molécule fille égale à 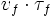{v}_{f} \cdot \tau_{f}. Où vOH est donnée par vf = vp + ve avec ve: vitesse d'éjection

Le flux de molécules filles, étant formées dans la couche [X,X+dX] est donc

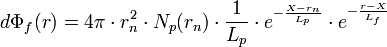
d\Phi_{f}(r) = 4\pi \cdot r_n ^2 \cdot N_p (r_n) \cdot \frac{1}{L_p} \cdot e ^ {-\frac{X-r_n}{L_p}} \cdot e ^ {-\frac{r - X}{L_{f}}}

En intégrant sur dX, on obtient le flux total à la distance r du noyau :

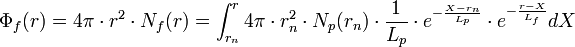
\Phi_{f}(r) =4\pi \cdot r ^2 \cdot N_{f} (r) = \int _{r_n} ^r 4\pi \cdot r_n ^2 \cdot N_p (r_n) \cdot \frac{1}{L_p} \cdot e ^ {-\frac{X-r_n}{L_p}} \cdot e ^ {-\frac{r - X}{L_{f}}} dX

on utilise les identités :

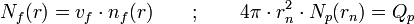
N_{f}(r)=v_{f} \cdot n_{f}(r) \qquad ; \qquad 4\pi \cdot r_n ^2 \cdot N_p (r_n) = Q_p

le calcul de l'intégrale ainsi fait donne finalement la distribution radiale de densité des molécules filles:

n_{f} (r) = \frac{Q_p}{4\pi r ^2 v_{f}} \frac{L_{f}}{L_{f}-L_p}\cdot \Big[ e^{-\frac{ r }{L_{f}}} -e ^{-\frac{ r }{L_p}} \Big]

C'est la formule de Haser pour les molécules-filles.

Une autre façon d'exprimer cette densité est de remplacer les longueurs d'échelle Lp,LOH par les taux de vie correspondants et les distances r par t. Finalement, ce ne serait qu'une autre façon d'exprimer la même chose.

Interprétation des observations

Lorsqu'une comète est observée par un spectroscope au sol ou dans l'espace, un spectre est obtenu. A partir de ce spectre on identifie les molécules présentes dans l'« atmosphère » de la comète.

Très souvent, les signatures spectrales des molécules mères (telles que H2O, CO2, HCN, CH4) sont faibles voire inobservables au sol. On se sert donc des observations de molécules filles (comme le radical OH- issu de l'eau) qui ont des raies spectrales fortes et plus facilement détectables. A partir de là, on peut remonter à la quantité des molécules premières pour estimer leur quantité et leur taux production.

Correction du modèle

Les défauts

Le modèle de Haser présente quelques défauts de taille.

  • Premièrement, les comètes ayant un noyau sphérique n'ont jamais été observées, la symétrie sphérique est loin d'être respectée. La forme du noyau cométaire ressemble plus à une pomme de terre.

Il en découle que la distribution des vitesses n'est pas forcément radiale.

  • Deuxièmement, le processus de dissociation d'une molécule-mère en molécule-fille est isotrope et non radial.

Cela conduit à des sous-estimations des longueurs d'échelle caractéristiques.

Notes et références

  1. ↑ L. Haser "Distribution d'intensité dans la tête d'une comète", 1957, Bulletin de l'académie royale de Belgique.
  • Portail de l’astronomie Portail de l’astronomie
Ce document provient de « Mod%C3%A8le de Haser ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Modèle de haser de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Modèle de Haser — Le modèle de Haser[1] est très souvent utilisé pour interpréter les résultats d observation des comètes. Supposant une forme sphérique du noyau, ce modèle permet de donner une estimation correcte et rapide de quantité d eau (ou autres molécules… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”