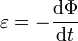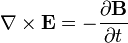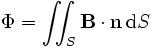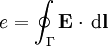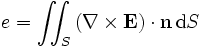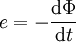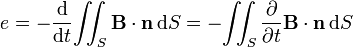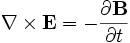Loi de Lenz

Loi de Lenz

Loi de Lenz-Faraday

En physique, la loi de Lenz-Faraday, ou loi de Faraday explique les phénomènes macroscopiques d'induction électromagnétique. Elle est aujourd'hui généralisée, dans la théorie de l'électromagnétisme, sous la forme de l'équation locale de Maxwell-Faraday. Elle est fondée sur les travaux de Michael Faraday en 1831, et sur l'énoncé de Heinrich Lenz de 1834.

Dans le langage courant, il y est fait allusion afin de décrire tout phénomène se produisant à l'opposé de l'intention de l'utilisateur; en particulier lorsque les effets résultants contrarient celui-ci.

Sommaire

Énoncé

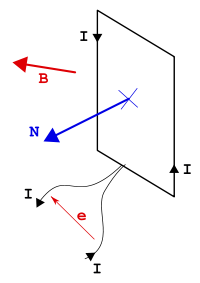
Orientation du flux et de la tension induite

La forme intégrale, historique, de la loi de Lenz-Faraday était au départ empirique. Un circuit soumis à un flux magnétique Φ (issu d'un champ magnétique variable H) subit une force électromotrice \varepsilon (mesurée en convention générateur) telle que :

\varepsilon = - \frac{\mathrm d \Phi}{\mathrm dt}

Le signe « - » présent dans cette loi, est dû au fait que l'induction produit des effets qui s'opposent à leurs causes. Un exemple de cette loi est donné par les courants de Foucault.

Forme locale

Dans sa forme locale, due à James Clerk Maxwell, on peut l'écrire :

\nabla \times \mathbf E = - \frac{\partial \mathbf B}{\partial t}

avec E le champ électrique, B le champ magnétique et \nabla l'opérateur formel nabla, qui calcule ici le rotationnel du champ E. Cette relation est appelée équation de Maxwell-Faraday, ou équation locale de Faraday.

La forme locale, qui constitue l'une des quatre équations de Maxwell est posée comme postulat de l'électromagnétisme. Néanmoins, il est possible de vérifier que les deux formes, intégrale et locale, sont équivalentes. Posant comme point de départ la forme intégrale, on peut montrer la forme locale, et réciproquement.

Démonstration

Soit S une surface immobile quelconque de l'espace 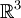{\mathbb{R}}^3, de normale 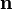\mathbf n. Cette surface est traversée par un champ magnétique dont on suppose la cause extérieure. Le flux de 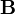\mathbf B à travers S est :

\Phi = \iint_S \mathbf B \cdot \mathbf n \, \mathrm dS

De plus, la force électromotrice e est égale à la circulation du champ électrique sur le contour Γ de S :

e = \oint_{\Gamma}\mathbf E \cdot \, \mathrm d \mathbf l

D'après le théorème de Stokes, on a :

e = \iint_{S} \left( \mathbf{\nabla} \times \mathbf E \right) \cdot \mathbf n \, \mathrm dS

Ainsi, la loi de Lenz-Faraday, qui s'écrit :

e = - \frac{\mathrm d\Phi}{\mathrm dt}

donne lieu à l'égalité suivante :

e = - \frac{\mathrm d}{\mathrm dt}{\iint_S\mathbf B \cdot\mathbf n \, \mathrm dS} = - {\iint_S\frac{\partial}{\partial t}\mathbf B\cdot\mathbf n \, \mathrm dS}

Nous avons maintenant 2 expressions intégrales de e, celles-ci étant valables quelle que soit la surface S, les intégrandes sont égaux, et on a :

\mathbf{\nabla} \times \mathbf{E} = - \frac{\partial \mathbf B}{\partial t}

qui n'est autre que l'équation de Maxwell-Faraday, et que l'on qualifie aussi d'équation locale de Faraday. La démarche exactement inverse montre que, posant cette dernière équation comme postulat, on retrouve la forme intégrale.

Voir aussi

Bibliographie

  • John David Jackson, Électrodynamique classique [« trad. de (en)Classical Electrodynamics »] 

Liens externes

  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
  • Portail de la physique Portail de la physique

Ce document provient de « Loi de Lenz-Faraday ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Lenz de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Loi De Lenz — Faraday En physique, la loi de Lenz Faraday, ou loi de Faraday explique les phénomènes macroscopiques d induction électromagnétique. Elle est aujourd hui généralisée, dans la théorie de l électromagnétisme, sous la forme de l équation locale de… …   Wikipédia en Français

  • Loi de lenz — Faraday En physique, la loi de Lenz Faraday, ou loi de Faraday explique les phénomènes macroscopiques d induction électromagnétique. Elle est aujourd hui généralisée, dans la théorie de l électromagnétisme, sous la forme de l équation locale de… …   Wikipédia en Français

  • loi de Lenz — ● loi de Lenz Loi selon laquelle le déplacement d un courant électrique ou d un aimant situés dans le voisinage d un circuit fermé y développe un courant induit qui tend à s opposer à la variation du flux inducteur. (→ induction électromagnétique …   Encyclopédie Universelle

  • loi de Lenz — Lenco taisyklė statusas T sritis fizika atitikmenys: angl. Lenz’s law; Lenz’s rule vok. Lenzsche Regel, f; Lenzsches Gesetz, n rus. закон Ленца, m; правило Ленца, n pranc. loi de Lenz, f …   Fizikos terminų žodynas

  • Loi de Lenz-Faraday — En physique, la loi de Lenz Faraday, ou loi de Faraday, permet de rendre compte des phénomènes macroscopiques d induction électromagnétique. Fondée sur les travaux de Michael Faraday en 1831, et sur l énoncé de Heinrich Lenz de 1834, elle est… …   Wikipédia en Français

  • Loi de Faraday-Lenz — Loi de Lenz Faraday En physique, la loi de Lenz Faraday, ou loi de Faraday explique les phénomènes macroscopiques d induction électromagnétique. Elle est aujourd hui généralisée, dans la théorie de l électromagnétisme, sous la forme de l équation …   Wikipédia en Français

  • Loi De Faraday — Loi de Lenz Faraday En physique, la loi de Lenz Faraday, ou loi de Faraday explique les phénomènes macroscopiques d induction électromagnétique. Elle est aujourd hui généralisée, dans la théorie de l électromagnétisme, sous la forme de l équation …   Wikipédia en Français

  • Loi de Faraday — Loi de Lenz Faraday En physique, la loi de Lenz Faraday, ou loi de Faraday explique les phénomènes macroscopiques d induction électromagnétique. Elle est aujourd hui généralisée, dans la théorie de l électromagnétisme, sous la forme de l équation …   Wikipédia en Français

  • Loi de Faraday pour l'induction — Loi de Lenz Faraday En physique, la loi de Lenz Faraday, ou loi de Faraday explique les phénomènes macroscopiques d induction électromagnétique. Elle est aujourd hui généralisée, dans la théorie de l électromagnétisme, sous la forme de l équation …   Wikipédia en Français

  • Loi de faraday — Loi de Lenz Faraday En physique, la loi de Lenz Faraday, ou loi de Faraday explique les phénomènes macroscopiques d induction électromagnétique. Elle est aujourd hui généralisée, dans la théorie de l électromagnétisme, sous la forme de l équation …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”