- Logique Temporelle
-
Logique temporelle
Les différentes logiques temporelles sont des logiques mathématiques et plus précisément des logiques modales. Intuitivement, cela signifie que la notion de vérité dans ces logiques dépend de l'évolution du monde. C'est-à-dire qu'une proposition peut-être, à un moment, fausse puis, plus tard, devenir vrai, etc.
Définition
Ces logiques sont donc définies sur un ensemble de propositions atomiques P ou variables de propositions. Ces propositions atomiques sont combinées par un certain nombre de connecteurs logiques, dont les connecteurs classiques : et, ou, non, implication, ainsi que d'autres opérateurs que l'on appelle des modalités. La logique temporelle est donc une logique modale. Dans le cas de la logique temporelle linéaire (LTL), on ajoute les modalités suivantes.
- X : demain ou immédiatement après (à distinguer donc du don't care en logique classique noté aussi X)
- F : un jour
- G : toujours
- U : jusqu'à
- R : release
Une formule de logique des propositions classique, comme par exemple la formule (a et b) ou c sur l'ensemble de propositions P={a,b,c}, associe une valeur de vérité, vrai ou faux, à chaque sous-ensemble de P. Par cette formule exemple, le sous-ensemble {a} est faux, le sous-ensemble {b,c} est vrai.
Une formule de logique temporelle associe une valeur de vérité non pas à chaque partie de P, mais selon le type de logique, à chaque suite de parties de P ou à chaque arbre sur les parties de P. Une logique définie sur les suites est dite linéaire, tandis qu'une formule définie sur les arbres est dite branching logic ou logique à embranchements.
Prenons le cas des logiques linéaires. Une telle logique associe donc une valeur de vérité, vrai ou faux, à chaque suite
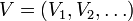telle que chaque Vi soit une partie de P. Notons M une telle formule, nous avons :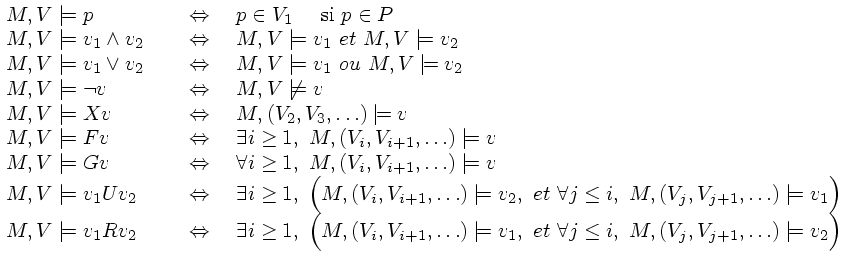
Intuitivement, si la suite V représente l'évolution dans le temps des différentes propositions de P, alors
- X(f) est vraie maintenant si f est vraie à partir de l'étape suivante,
- F(f) est vraie maintenant si f est vraie à au moins une étape ultérieure,
- G(f) est vraie maintenant si f est vraie à toutes les étapes suivantes y compris maintenant,
- f1 U f2 est vraie si f1 est vraie (y compris) jusqu'à ce que f2 soit vraie,
- f1 R f2 est vraie si f2 est vraie (y compris) jusqu'à ce que f1 soit vraie.
Articles connexes
Portail de la logique
Catégories : Logique modale | Méthode formelle
Wikimedia Foundation. 2010.
