- Les Quatre Quatre
-
Les quatre quatre
Le problème des quatre quatre est un problème récréatif arithmétique : « Quels sont les entiers que l'on peut écrire en utilisant quatre fois le chiffre quatre et les opérations usuelles ? »
Ce problème, appelé en anglais Four 4's Puzzle, semble avoir été publié pour la première fois par écrit dans un ouvrage de W. W. Rouse Ball, Mathematical Recreations and Essays, paru en 1892. Ball le décrit comme une récréation mathématique traditionnelle.
La suite des entiers consécutifs commençant à zéro atteinte par ce protocole dépend des contraintes données au problème.
Avec quatre nombres 4 et quatre opérations
Il est facile de prouver, en étudiant tous les cas, que pour 4 fois le nombre 4 et les quatre opérations élémentaires, il est possible d'obtenir tous les entiers naturels de 0 à 9, mais qu'il n'est pas possible d'obtenir 10 ni 11.
- 0 = 4/4 - 4/4
- 1 = 4/4+(4-4)
- 2 = 4/4 + 4/4
- 3 = (4 + 4 +4)/4
- 4 = 4 + (4-4) × 4
- 5 = (4 × 4 + 4)/4
- 6 = 4 + (4 + 4)/4
- 7 = 4 + 4 - 4/4
- 8 = 4 + 4 + (4 - 4)
- 9 = 4 + 4 + 4/4
Avec quatre chiffres 4 et plus d'opérations
Il est fréquent de rencontrer ce problème avec des conditions moins restrictives : possibilité d'écrire des nombres formés de chiffres 4, ajout de la racine carrée, de l'exposant et de la factorielle.
Le champ des valeurs atteintes s'agrandit alors
- 10 = (44 - 4) / 4
- 11 = 44/(√4 + √4)
- 12 = (4 - 4/4) x 4
- ...
Il semble que l'on puisse alors aller jusqu'à 74 (= 4! + 4! + 4! + √4)
En admettant des écritures comme .4, (pour 0,4) ,
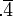(pour 4/9) et la fonction gamma, il semble que l'on puisse aller bien au-delà.Enfin, il est amusant de prouver qu'avec la fonction log, tout entier est accessible :
Par exemple :
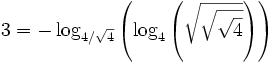
Liens externes
- (fr) Site de Gérard Villemin
- (en) The Definitive Four Fours Answer Key, David A. Wheeler
- (en) The Four Fours Problem Université de Toronto.
- (fr) Site de Géry Huvent
Portail des mathématiques
Catégorie : Mathématiques récréatives
Wikimedia Foundation. 2010.
